Snelliussches Brechungsgesetz

Das snelliussche Brechungsgesetz, auch snelliussches Gesetz, Snell-Gesetz, oder vereinfacht Brechungsgesetz, besagt, dass eine Welle (z. B. ein Lichtstrahl) ihre Richtung ändert – man sagt gebrochen wird – wenn sie von einem transparenten Medium in ein anderes transparentes Medium auf Grund unterschiedlicher Materialeigenschaften (wie der Dichte) mit einer anderen Phasengeschwindigkeit übergeht. Das Gesetz gilt für alle Wellenarten. Es besagt nur, in welche Richtung die Welle abgelenkt wird, nicht aber, wie viel von der Welle an dem Übergang zwischen den beiden Medien transmittiert bzw. reflektiert wird. Im Fall der Totalreflexion ist das reelle Brechungsgesetz ungültig. Es muss dann komplex gerechnet werden. Wie viel Licht transmittiert bzw. reflektiert wird, ergibt sich aus den Fresnel-Formeln.

Reflexion und Brechung eines Lichtstrahls an einem Glasprisma

Geschichte

Brechung wurde von Ptolemäus in seiner 'Optik' beschrieben, sein Gesetz gilt aber nur für kleine Winkel. Das Brechungsgesetz wurde zum ersten Mal im 10. Jahrhundert von Ibn Sahl korrekt angegeben. 1601 wurde es von Thomas Harriot wiederentdeckt, aber nicht veröffentlicht. 1618 wurde es von dem Holländer Willebrord van Roijen Snell und fast zur gleichen Zeit von René Descartes beschrieben.

Beschreibung

Zur Herleitung des Brechungsgesetzes

Wellenfronten, die von einem Punkt ausgehen. Das Material unter der grauen Linien hat einen höhere Brechungsindex, die Phasengeschwindigkeit der Welle ist dort geringer.

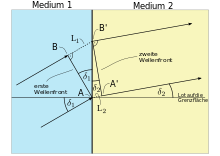
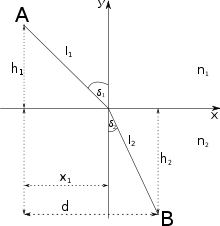
Das nebenstehende Bild zeigt einen Lichtstrahl, der aus dem Medium₁ (z. B. Luft) auf die Grenzfläche eines Mediums₂ (z. B. Glas) einfällt. Er ist dabei um den Winkel δ₁ gegen das Einfallslot geneigt. Ein Teil des Lichtstrahls wird an der Oberfläche reflektiert, der Rest tritt unter Richtungsänderung (Brechung) ein und läuft dort unter dem Winkel δ₂ gegen das Lot weiter. Dieser Vorgang wird durch das Snell-Gesetz beschrieben.

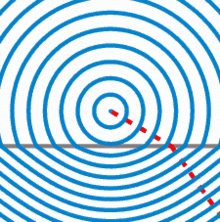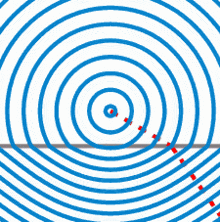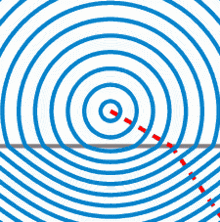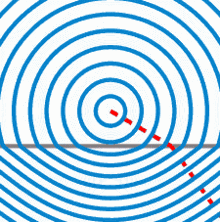
Die Wellenfronten von Licht bewegen sich durch ein Medium mit einer Geschwindigkeit, die vom Brechungsindex des Mediums abhängt. Der Brechungsindex n gibt das Verhältnis der Lichtgeschwindigkeit c von Licht im Vakuum zur Phasengeschwindigkeit von Licht im Medium an.

$n = \frac{c}{c_{\rm Medium}}$,

Dabei ist der Brechungsindex eine Materialeigenschaft des Mediums, die von der Frequenz des Lichts, der Polarisation, der Intensität und von der Richtung abhängen kann, in der das Licht das Medium durchquert.

Werden zwei parallel einfallende Lichtstrahlen an einer idealen Grenzfläche zweier Medien betrachtet, ergibt sich geometrisch für den zweiten Strahl eine zusätzliche Wegstrecke L₁ = c₁t im Medium 1 sowie für den ersten Lichtstrahl eine zusätzliche Wegstrecke L₂ = c₂t im Medium 2 (hierbei sind c_1,2  die Ausbreitungsgeschwindigkeiten im jeweiligen Medium; t die zusätzliche Laufzeit). Über Winkelbeziehungen im rechtwinkligen Dreieck ergibt sich:

$\sin(\delta_1) = \frac{L_1}{\overline {AB'}}$ bzw. $\sin(\delta_2) = \frac{L_2}{\overline {AB'}}$

wobei δ₁ bzw. δ₂ der Einfalls- bzw. Brechungswinkel und $\overline {AB'}$ der Abstand der beiden Lichtstrahlen ist.

Ersetzt man den Abstand $\overline {AB'}$ in Medium 1 durch den Zusammenhang in Medium 2, ergibt sich:

$\frac{\sin(\delta_1)}{\sin(\delta_2)} = \frac{L_1}{L_2}$

Winkelabhängigkeit bei der Brechung für die Medien Luft, Wasser und Glas

Mit den Zusammenhängen für die Wegstrecke und der abhängigen Ausbreitungsgeschwindigkeit erhält man das Brechungsgesetz:

$\frac{\sin(\delta_1)}{\sin(\delta_2)}= \frac{c_1 t}{c_2 t} = \frac{c_1}{c_2}=\frac{n_2}{n_1}$

wobei n₁ und n₂ die Brechungsindizes der jeweiligen Medien sind.

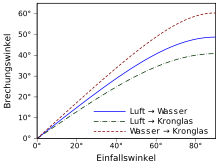
Somit erhält man den in der Grafik rechts dargestellten Zusammenhang zwischen den Winkeln δ₁ und δ₂:

$\delta_2 = \arcsin\left(\frac{\sin(\delta_1)\, n_1}{n_2}\right)$.

Im allgemeinen wird der Eintritts- und Austrittswinkel von Strahlen immer vom Lot aus, dass auf der Grenzfläche steht, gezählt. Diese Winkel entsprechen den bei der Herleitung verwendeten Winkeln und damit ergibt sich das Brechungsgesetz in der konventionellen Form zu

n₁sin(δ₁) = n₂sin(δ₂).

Für absorbierende Medien, für die der Brechungindex als komplexe Zahl definiert ist, kann das Brechungsgesetz in der einfachen Form im allgemeinen nicht angewendet werden. Dies funktioniert nur, wenn der Imaginärteil viel kleiner als der Realteil ist.^[1]

Die Auffächerung von weißem Licht durch ein Prisma kann mit dem Brechungsgesetz unter Zunahme eines wellenlängenabhängigen Brechungsindex erklärt werden (siehe 3. Grafik rechts). In einem Prisma ist der Brechungsindex wellenlängenabhängig, was zu unterschiedlichen Austrittswinkeln der einzelnen Spektralkomponenten des weißen Lichts führt.

Herleitung aus dem fermatschen Prinzip

Herleitung aus dem fermatschen Prinzip

Rettungsschwimmer bewegen sich am Strand schneller fort als im Wasser. Das hat zur Folge, dass die „Front“ von vier Rettungsschwimmern ihre Richtung ändert, wenn sie vom Strand ins Wasser kommen. Dies entspricht der Brechung einer Welle am optisch dichteren Medium.

Das Brechungsgesetz ist eine Folgerung des fermatschen Prinzips, das besagt, dass der optische Weg zwischen zwei Punkten stationär (also minimal, maximal oder ein Sattelpunkt) sein muss. In diesem Falle gilt, dass der optische Weg wirklich minimal wird, da sich die Strahlengänge nicht kreuzen. Der Beweis berechnet den optischen Weg (OW) zwischen den Punkten A (im Medium 1) und B (im Medium 2) in Abhängigkeit von der Lage von x₁. Der minimale optische Weg wird berechnet, indem dessen Ableitung null gesetzt wird.

$OW(A \rightarrow B) = n_1 \, l_1 + n_2 \, l_2$

Nach dem Satz des Pythagoras folgt:

$n_1l_1 + n_2l_2 = n_1\sqrt{{h_1}^2 + {x_1}^2} + n_2\sqrt{{h_2}^2 + (d-{x_1})^2}$

Setzt man dessen Ableitung nach x₁ null, erhält man

$\frac{\mathrm{d}OW}{\mathrm{d}{x_1}} = n_1 \frac{{x_1}}{\sqrt{{h_1}^2 + {x_1}^2}} - n_2\frac{d-{x_1}}{\sqrt{{h_2}^2 + (d-{x_1})^2}}$

$= n_1 \frac{{x_1}}{l_1} - n_2\frac{d-{x_1}}{l_2} = n_1\sin(\delta_1) -n_2\sin(\delta_2) = 0$

und daher n₁sin(δ₁) = n₂sin(δ₂), was der oben genannten Formulierung entspricht.

Veranschaulichungen

Deutung mit dem fermatschen Prinzip

Das Licht wählt den Weg, auf dem es am schnellsten von Punkt A zum Punkt B kommt. Ein Beispiel hierfür ist etwa der Rettungsschwimmer, der sich am Strand schneller fortbewegen kann als im Wasser. Welchen Weg muss er von A aus nehmen, um möglichst schnell bei dem in Not geratenen Schwimmer B anzukommen? Es ist nicht der direkte Weg von A nach B, da er dann sehr weit im langsameren Medium (Wasser) unterwegs ist. Es ist auch nicht der Weg, bei dem der Rettungsschwimmer senkrecht zum Strand in Richtung B schwimmt, da dann der Weg am Strand sehr lang ist. Der schnellste Weg liegt dazwischen.

Drehung der Wellenfront

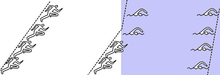
Rettungsschwimmer bewegen sich am Strand schneller fort als im Wasser. Das hat zur Folge, dass die „Front“ von vier Rettungsschwimmern ihre Richtung ändert, wenn sie vom Strand ins Wasser kommen. Dies entspricht der Brechung einer Welle am optisch dichteren Medium.

Allerdings wird bemängelt, dass der Vergleich mit den Rettungsschwimmern hinkt, da sich zwar ihre „Front“ dreht, ihre Ausbreitungsrichtung aber nicht. Würde der Vergleich mit den Schwimmern auch für die Welle gelten, so würde die Welle eine Schräglage zur Ausbreitungsrichtung einnehmen.

Literatur

• Eugene Hecht: Optik. 4. Auflage. Oldenbourg Wissenschaftsverlag, München, ISBN 3486273590.

Weblinks

• Brechungsgesetz für Schüler (LEIFI)

Einzelnachweise

1. ↑ Torsten Fließbach: Elektrodynamik. Lehrbuch zur Theoretischen Physik II. 4. Auflage. Spektrum Verlag, 2004. ISBN 3-8274-1530-6 (Kapitel 36).