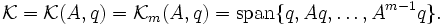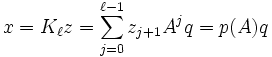Krylow-Unterraum

Ein Krylowraum ist ein Untervektorraum des komplexen Spaltenvektorraums 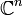$\mathbb{C}^n$, der zu einer quadratischen Matrix 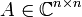$A\in\mathbb{C}^{n\times n}$, einem Spaltenvektor 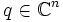$q\in\mathbb{C}^n$, dem Startvektor der Krylow-Sequenz und einem Index m als lineare Hülle iterierter Matrix-Vektor-Produkte definiert ist:

$\mathcal{K}=\mathcal{K}(A,q) =\mathcal{K}_m(A,q) =\mbox{span}\{q,Aq,\ldots,A^{m-1}q\}.$

Dimension des Krylowraumes

Die Dimension des Krylowraumes 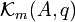$\mathcal{K}_m(A,q)$ ist einerseits beschränkt durch die Anzahl m der erzeugenden Elemente, andererseits durch die Dimension n des umgebenden Spaltenvektorraums. Es gibt somit einen maximalen Index 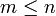$m\le n$, bis zu dem die Dimension des Krylowraumes mit seinem Index übereinstimmt. Dies bedeutet, dass der Vektor A^mq von den vorhergehenden Erzeugenden linear abhängig wird, d.h. 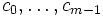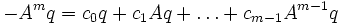dass es Konstanten $c_0,\dots,c_{m-1}$ mit $-A^mq=c_0q+c_1Aq+\dots+c_{m-1}A^{m-1}q$ gibt. Aus dieser Identität folgt, dass auch alle nachfolgenden Erzeugenden A^{m + k}q von den ersten m linear abhängig sind, d.h. die Folge der Dimensionen der Krylowräume wird bei m konstant.

Den minimalen Index m, für den der Raum nicht mehr erweitert wird, nennt man den Grad von q in A. An diesem Punkt brechen die meisten Krylowraum-Verfahren mit der exakt berechneten Lösung ab. Wie man am Beispiel eines Eigenvektors von A als Startvektor erkennen kann, kann dieses Ereignis deutlich vor n, der Dimension des Gesamtraumes stattfinden.

Krylowräume und Polynome

So lange der minimale Index m nicht erreicht wurde, lassen sich Vektoren 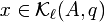$x\in\mathcal{K}_\ell(A,q)$ eindeutig durch Polynome der Form p(A)q vom Höchstgrad 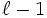$\ell-1$ beschreiben. Sei dazu die Krylowmatrix 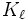$K_\ell$ definiert durch 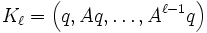$K_\ell=\left(q,Aq,\ldots,A^{\ell-1}q\right)$. Dann lässt sich x darstellen als 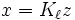$x=K_\ell z$ für einen Koeffizientenvektor 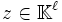$z\in\mathbb{K}^\ell$. Einsetzen zeigt, dass

$x=K_\ell z=\sum_{j=0}^{\ell-1} z_{j+1} A^j q = p(A)q$

für ein Polynom vom Höchstgrad 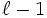$\ell-1$ gilt. Diese Umschreibung stellt also eine Bijektion dar.

Für 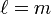$\ell=m$ gibt es Polynome p minimalen Grades m-1, die den Nullvektor ergeben, p(A)q = 0. Diese Polynome sind immer Faktoren des charakteristischen Polynoms χ_A. Die Eigenwerte, die den Nullstellen eines Faktors kleinen Grades entsprechen, sind einfacher aus diesem als aus dem gesamten charakteristischen Polynom zu bestimmen.

Die Identität p(A)q = 0 kann in die Form 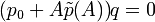$\big(p_0+A\tilde p(A)\big)q=0$ umgeschrieben werden, d.h.

$q=-\frac1{p_0}A\tilde p(A)q=A\cdot\left(\frac1{p_0}(-p_1-p_2A-\dots-p_{m-1}A^{m-2})q\right)$.

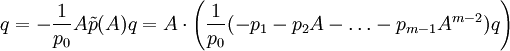Der zweite Faktor 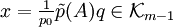$\textstyle x=\frac1{p_0}\tilde p(A)q\in\mathcal K_{m-1}$ auf der rechten Seite ist eine Lösung des linearen Gleichungssystems Ax=q.

Vorkommen

Krylowräume bilden die Grundlage für einige Projektionsverfahren, die sogenannten Krylow-Unterraum-Verfahren. Benannt sind Krylowräume nach dem russischen Schiffsbauingenieur und Mathematiker Alexei Nikolajewitsch Krylow, welcher sie in einem 1931 erschienenen Artikel zur Eigenwertberechnung über das charakteristische Polynom verwendete. Der von Krylow gefundene Algorithmus hat nicht mehr viel mit den heutzutage verwendeten Krylowraum-Verfahren gemein, wird aber in der Computeralgebra und insbesondere in Computeralgebrasystemem (CAS) verwendet.

Literatur

• Y. Saad: Iterative Methods for Sparse Linear Systems, 2nd edition, SIAM Society for Industrial & Applied Mathematics 2003, ISBN 0-898-71534-2