Krylov-Unterraum-Verfahren

Krylow-Unterraum-Verfahren sind iterative Verfahren zum Lösen großer, dünnbesetzter linearer Gleichungssysteme, wie sie bei der Diskretisierung von partiellen Differentialgleichungen entstehen oder von Eigenwertproblemen. Sie sind benannt nach dem russischen Schiffsbauingenieur und Mathematiker Alexei Nikolajewitsch Krylow, der die Krylow-Unterräume definierte. Mit den hier beschriebenen Verfahren hat das von ihm entwickelte Verfahren zur Berechnung der Koeffizienten des charakteristischen Polynomes nicht mehr viel zu tun. Die Verfahren sind sogenannte Black-Box-Verfahren, die sich durch einfache Implementierung und Robustheit auszeichnen, weshalb sie vielfach verwendet werden. Die Verfahren sind fast alle Projektions-Verfahren.

Die Verfahrensklasse

Gegeben ist das lineare Gleichungssystem 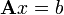$\mathbf{A}x=b$ mit der Matrix 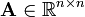$\mathbf{A} \in \mathbb{R}^{n \times n}$. Zu einer beliebigen Näherungslösung x₀ für x und dem Residuum 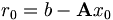$r_0=b-\mathbf{A}x_0$ ist der m-te Krylow-Unterraum 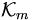${\mathcal K}_m$ der von den Vektoren 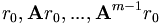$r_0, \mathbf{A}r_0, ..., \mathbf{A}^{m-1}r_0$ aufgespannte Untervektorraum.

Fast alle Verfahren finden nun eine bessere Näherungslösung 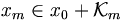$x_{m} \in x_{0}+{\mathcal K}_m$ mit der Bedingung, dass der Vektor 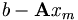$b-\mathbf{A} x_{m}$ orthogonal zu allen Vektoren eines Unterraumes 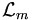${\mathcal L}_m$ steht, eine so genannte Projektion. Diese Bedingung heißt Galerkin-Bedingung.

Damit ist das Problem auf ein m-dimensionales lineares Gleichungssystem reduziert. Das Ganze wird zu einem iterativen Lösungsverfahren, wenn man die Dimension in jedem Schritt um eins erhöht.

Spezielle Lösungsverfahren ergeben sich durch die konkrete Wahl des Raumes 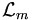${\mathcal L}_m$, sowie durch Ausnutzen von speziellen Eigenschaften der Matrix A, was das Verfahren beschleunigt, aber die Anwendbarkeit auch einschränkt. Die einfachste Variante ist, für 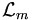${\mathcal L}_m$ einfach wieder den Krylow-Unterraum selbst zu wählen. Das besondere an den Verfahren ist, dass sie nur Matrix-Vektor-Multiplikationen sowie Skalarprodukte benötigen. Ist die Matrix dünnbesetzt, so ist das Matrix-Vektor-Produkt schnell ausrechenbar und der Algorithmus praktikabel.

Ein Beispiel ist das Verfahren der Konjugierten Gradienten (CG-Verfahren). Hierbei ist 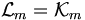${\mathcal L}_m={\mathcal K}_m$ und es ist für symmetrische, positiv definite Matrizen gedacht.

Man erhält so einen großen Zoo an Verfahren. Viel wichtiger als die Auswahl der speziellen Krylow-Unterraummethode ist die Wahl des Vorkonditionierers. Dieser formt das lineare Gleichungssystem äquivalent um, so dass die Lösung unverändert bleibt, sich aber günstigere Eigenschaften für die Konvergenz ergeben. Hier sind entscheidende Geschwindigkeitsgewinne zu erzielen, die dazu führen, dass selbst Systeme mit Millionen Unbekannten in wenigen Dutzend Schritten zufriedenstellend gelöst werden können.

Aufwand

Die Verfahren zeichnen sich dadurch aus, dass nur Matrix-Vektor-Multiplikationen und Skalarprodukte im Ablauf benötigt werden. Die Matrix-Vektor-Multiplikation kostet bei einer dünnbesetzten Matrix mit O(n) Einträgen nur O(n) arithmetische Operationen. Damit liegt der Gesamtaufwand bei m << n Iterationen immer noch bei O(n), allerdings mit einer sehr hohen Konstante. Entsprechend sind Krylow-Unterraum-Verfahren für vollbesetzte Matrizen nicht geeignet und für dünnbesetzte Matrizen erst ab einer gewissen Größe, in etwa einigen zehntausend Unbekannten.

Geschichte

Die ersten Krylow-Unterraumverfahren waren das Lanczos-Verfahren, das 1950 und 1952 von Cornelius Lanczos, das Arnoldi-Verfahren, das 1951 von Walter Edwin Arnoldi, und das CG-Verfahren, dass 1952 von Magnus Rudolph Hestenes und Eduard Stiefel veröffentlicht wurde. Die meisten Krylow-Unterraumverfahren sind sogar direkte Löser, die nach spätestens n Schritten bei exakter Arithmetik die exakte Lösung reproduzieren. Allerdings sind die Verfahren als direkte Löser aufgrund Instabilität bei Rundungsfehlern ungeeignet. Der Nutzen als iterativer Löser wurde damals noch nicht erkannt und so verschwanden die Verfahren in der Schublade. Anfang der 1970er wurde der Nutzen des CG-Verfahrens mit Präkonditionierung dann von Reid erkannt und 1971 eine bestechende Fehleranalyse des symmetrischen Lanczos-Verfahrens von Christopher Conway Paige gegeben. Daraufhin entstand eine Vielzahl an neuer, besserer und stabilerer Verfahren wie MinRes, SymmLQ, GMRES und QMR und gänzlich neue Krylow-Unterraumverfahren wie CGS, BiCG, BiCGSTAB und TFQMR wurden entwickelt. Die heutige Klassifizierung der Krylow-Unterraumverfahren nach den Ansätzen QOR und QMR, sowie Verallgemeinerungen vom CG-Verfahren nach den Ansätzen Orthores, Orthomin und Orthodir begannen Ende der 1970er.

Inzwischen gibt es angepasste Krylow-Unterraumverfahren für nichtlineare Eigenwertrobleme, wie den rationalen Krylow von Axel Ruhe und den nichtlinearen Arnoldi von Heinrich Voss. Es existieren auch seit geraumer Zeit Verfahren, welche zur Lösung von nichtlinearen Gleichungssystemen in der inneren Schleife eines Newton-Verfahrens Krylow-Unterraumverfahren verwenden, subsumiert unter dem Schlagwort Newton-Krylow-Methoden oder bei Erwähnung des Vorkonditionieres beispielsweise Newton-Krylow-Schwarz-Methoden.

Alphabetische Liste gängiger Krylow-Unterraum-Verfahren

• Arnoldi-Verfahren, zur Eigenwertapproximation
• BiCG, das CG-Verfahren für nicht SPD-Matrizen
• BiCGSTAB, Stabilisierung von CGS
• BiCGSTAB(ell), Stabilisierung von CGS
• BiCGSTABTFQMR, der Ansatz hinter TFQMR angewandt auf BiCGSTAB
• BiOres, eine Variante des BiCG-Verfahrens
• BiOmin, eine Variante des BiCG-Verfahrens
• BiOdir, eine Variante des BiCG-Verfahrens
• CG, zur approximativen Lösung linearer Gleichungssysteme
• CGNE, CG-Verfahren auf den Normalgleichungen, Variante 1
• CGNR, CG-Verfahren auf den Normalgleichungen, Variante 2
• CGS-Verfahren, quadrierte BiCG-Rekursion
• FOM, zur approximativen Lösung linearer Gleichungssysteme
• GMRES, zur approximativen Lösung linearer Gleichungssysteme
• Hessenberg-Verfahren, zur Eigenwertapproximation
• Lanczos-Verfahren, zur Eigenwertapproximation
• MinRes, zur approximativen Lösung linearer Gleichungssysteme
• Orthores, Orthomin und Orthodir, Verallgemeinerungen des CG-Verfahrens
• Ores, eine Variante des CG-Verfahrens
• Omin, eine Variante des CG-Verfahrens
• Odir, eine Variante des CG-Verfahrens
• Potenzmethode, älteste Methode zur Eigenwertapproximation
• QMR, zur approximativen Lösung linearer Gleichungssysteme
• Richardson-Iteration, bei geeigneter Interpretation
• SymmLQ, zur approximativen Lösung linearer Gleichungssysteme
• TFQMR, zur approximativen Lösung linearer Gleichungssysteme

Literatur

• A. Meister: Numerik linearer Gleichungssysteme, 2. Auflage, Vieweg 2005, ISBN 3528131357

• Y. Saad: Iterative Methods for Sparse Linear Systems, 2nd edition, SIAM Society for Industrial & Applied Mathematics 2003, ISBN 0-898-71534-2

Weblinks

• Y. Saad: Iterative Methods for Sparse Linear Systems, 1st edition, PWS 1996

• Templates for the Solution of Linear Systems