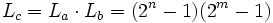LFSR

Ein linear rückgekoppeltes Schieberegister (engl. Linear Feedback Shift Register, kurz LFSR) ist ein rückgekoppeltes Schieberegister, welches zur Erzeugung von Pseudozufallszahlen eingesetzt werden kann.

Funktionsweise

Ein LFSR ist im Prinzip ein Schieberegister der Länge n. Jedoch wird im normalen Betrieb in jedem Takt das freiwerdende Bit am Eingang des Schieberegisters mit dem Ergebnis der XOR-Verknüpfung zweier oder mehrerer anderer Stellen des Schieberegisters in Form einer Rückkopplung (engl. Feedback) gefüllt. Bei geeigneter Wahl der Abzweigungen ist eine maximale Periodenlänge von bis zu 2ⁿ − 1 möglich, wobei n die Anzahl der Bits des Schieberegisters ist. Zur Initialisierung kann das Schieberegister mit beliebigen Werten gefüllt werden, nicht jedoch nur mit Nullen.

Animation für LFSR mit dem Polynom x¹⁶ + x⁵ + x³ + x² + 1

Als Sonderfall kann ein LFSR auch die maximale Periodenlänge von 2ⁿ aufweisen. In diesem Fall treten nach einem Durchlauf lauter '0' im Schieberegister auf, die durch eine zusätzliche Logik erkannt und durch Invertierung der Rückkopplung kompensiert werden müssen.

Ein LFSR bildet wegen seiner Linearität der erzeugten Folgen einen sehr schlechten Pseudozufallszahlengenerator. Er wird dabei in Verbindung mit nichtlinearen Funktionen verwendet um seine Sicherheit zu erhöhen.

Eine weitere Anwendungsmöglichkeit von LFSRs sind Modulo-Zähler, welche bis zur Periodenlänge zählen und dann "überlaufen" (also wieder von vorne beginnen). Dies ist deutlich effizienter als ein arithmetischer ("echter") Zähler, da statt einer n-Bit Addition lediglich einige XOR-Verknüpfungen notwendig sind. Allerdings lässt sich der aktuelle Zählerstand nicht direkt aus dem Zustand des LFSR ableiten, weshalb sich ein LFSR-Zähler nur für bestimmte Anwendungen eignet, z. B. zur Index-Berechnung eines FIFOs.

Zusammengesetzte Schieberegister

Eine Erweiterung stellt die Kombinationen der Datenfolgen verschiedenartiger LFSR dar. Die dabei entstehenden neuen Datenfolgen können andere Eigenschaften aufweisen. Sie können damit beispielsweise geeigneter für Anwendungen im Bereich CDMA sein.

Die Zusammensetzung der Ausgabedatenfolge aus den einzelnen unabhängigen LFSRs erfolgt meist mittels XOR-Verknüpfung der einzelnen Teilfolgen. Weisen die LFSR unterschiedliche Folgenlängen L = 2ⁿ-1 und unterschiedliche Generatorpolynome auf, lassen sich Codefolgen mit völlig neuen Eigenschaften erzeugen. Im Regelfall weisen diese zusammengesetzten, zyklischen Folgen nicht die maximal mögliche Länge auf. Im folgenden werden einige wichtige Klassen von aus LFSR-Registern zusammengesetzten Codefolgen dargestellt:

JPL-Folgen

JPL-Folgen bestehen aus zwei LFSRs deren Codefolgenlänge L_a und L_b teilerfremd sein müssen. In diesem Fall ist die Codefolgenlänge der erzeugten Gesamtfolge L_c gleich:

$L_c = L_a \cdot L_b = (2^n - 1)(2^m - 1)$

Es können auch mehr als zwei LFSRs mittels mehrfachen XOR am Ausgang zusammengeschaltet werden. Es müssen nur alle Codefolgelängen der einzelnen LFSR teilerfremd zueinander sein.

Entwickelt wurden JPL-Folgen in den Jet Propulsion Labs, wovon sich auch der Name für diese Codefolgen ableitet. Einsatzbereiche sind unter anderem im Bereich der Entfernungsmessung mittels Spread-Spectrum-Signalen bei Satelliten und in Bereich der Weltraumtechnik und bei dem militärisch genutzten und genaueren P/Y-Code im globalen Positionssystem GPS.

Gold-Folgen

Gold-Folgen wurden 1967 von Robert Gold vorgestellt und besitzen ebenfalls zwei LFSRs mit unterschiedlichen Generatorpolynomen allerdings von gleicher Länge m. Die maximale Codefolgenlänge der Gold-Folge ist daher auch nur 2^m-1. Hält man den Anfangszustand eines LFSR fest und verändert den Anfangszustand ("Phasenverschiebung") des anderen zyklisch, lassen sich 2^m-1 neue Codefolgen erstellen, die alle ein relativ großes periodisches Kreuzkorrelationsmaxium zueinander aufweisen, d. h. sie stehen fast orthogonal zueinander. Dies bedeutet, dass diese Codefolgen sich im Bereich des Codemultiplex (CDMA) verwenden lassen und damit eine Unterscheidung je nach verwendeter Gold-Folge ermöglichen.

Die Gold-Folgen sind auch wegen ihrer einfachen Erzeugung die in der Praxis am häufigsten eingesetzten Spread Spectrum-Signale. Anwendungsbereiche liegen neben Mobilfunksystemen (UMTS), welche mit CDMA arbeiten, auch bei dem zivil nutzbaren C/A-Code des globalen Positionssystems GPS und bei WLANs.

Siehe auch

• Maximum Length Sequence
• Berlekamp-Massey-Algorithmus
• Pseudozufallsrauschen