Leontieff-Produktionsfunktion

Die Leontief-Produktionsfunktion ist ein Typ (Typ B) der mikroökonomischen Produktionsfunktion. Sie wird als linear limitational bezeichnet, da die Produktionsfaktoren in einem festen Verhältnis zueinander und in einem festen Verhältnis zum Ausstoß (Output) eines Betriebes oder einer Anlage stehen. Die Ausbringungsmenge erreicht eine Limitation, wenn ein Produktionsfaktor nicht in ausreichendem Maße zur Verfügung steht.

In formaler Schreibweise gilt für die Funktion

$f: \mathbb{R}^n\longrightarrow\mathbb{R}^1, n\geq1, f(v) = a_0 \min \left\{\frac{v_1}{a_1},\frac{v_2}{a_2},\dots,\frac{v_n}{a_n}\right\}^{r}$

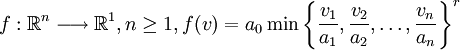
Die Leontief-Produktionsfunktion ist eine CES-Produktionsfunktion mit der Substitutionselastizität 0. Sie ist homogen mit dem Homogenitätsgrad r.

Beispiel

Jede 'rezeptmäßige' Produktion in der Küche oder im Labor ist Beispiel für die Leontief-Produktionsfunktion. Braucht man z.B. für einen Kuchen nach Rezept a₁ = 2 Eier, a₂ = 100g Mehl und a₃ = 0,1 Liter Milch, so kann man mit v₁ = 4 Eiern, v₂ = 300g Mehl und v₃ = 0,3 Litern Milch 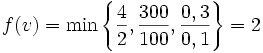$f(v) = \min \left\{\frac{4}{2},\frac{300}{100},\frac{0,3}{0,1}\right\}=2$ Kuchen produzieren. Limitational sind in diesem Fall die Eier, mit 6 Eiern hätte man 3 Kuchen produzieren können.

Die Produktionsfunktion geht zurück auf Wassily Leontief. Sie bildet die Grundlage der Input-Output-Analyse.

Siehe auch

• Produktion
• Gutenberg-Produktionsfunktion