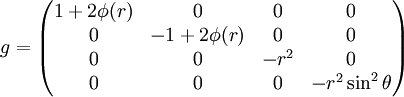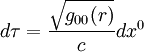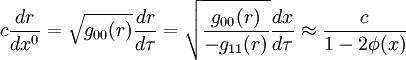Lichtkrümmung

Als Shapiro-Verzögerung, benannt nach Irwin I. Shapiro, bezeichnet man in der Allgemeinen Relativitätstheorie den Effekt, dass sich Licht in der Nähe einer großen Masse für einen weit entfernten Beobachter langsamer als mit Vakuumlichtgeschwindigkeit zu bewegen scheint.

Mithilfe der Shapiro-Verzögerung lässt sich auch die Lichtablenkung durch große Massen, der sogenannte Gravitationslinseneffekt, erklären.

Effekt

Für schwache, zeitunabhängige Gravitationsfelder erhält man als Näherung für die Metrik in Kugelkoordinaten

$g = \begin{pmatrix} 1+2\phi(r) & 0 & 0 & 0 \\ 0 & -1+2\phi(r) & 0 & 0 \\ 0 & 0 & -r^2 & 0 \\ 0 & 0 & 0 & -r^2 \sin^2{\theta} \end{pmatrix}$

Die Näherung lässt sich zum Beispiel gut an der Oberfläche eines Sterns verwenden, an der Oberfläche eines sehr viel dichteren Neutronensterns ist sie jedoch nicht so gut anwendbar und es gibt messbare Abweichungen. Bei der Anwendung auf einen Stern ist 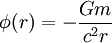$\phi (r) = -\frac{Gm}{c^2r}$ das Gravitationspotential, wobei m die Masse des Sterns, G die newtonsche Gravitationskonstante und c die Lichtgeschwindigkeit ist.

Mit dieser Näherung lässt sich anschaulich die Lichtablenkung durch Gravitation als Brechungseffekt interpretieren. Dazu muss man sich überlegen, was die reale Zeit an einem Raumzeitpunkt ist. Wir definieren für ein winziges Zeitintervall dτ:

$d\tau = \frac{\sqrt{g_{00}(r)}}{c} dx^0$

als die von einem Beobachter am Raumzeitpunkt x gemessene reale Zeit oder Eigenzeit. Außerdem muss man die Längenkontraktion berücksichtigen und die Länge x nahe der Masse definieren als

$dx = \sqrt{-g_{11}(r)} dr$.

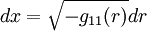Betrachten wir jetzt einen Lichtstrahl so ist seine reale Geschwindigkeit 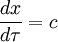$\frac{dx}{d\tau} = c$ die Vakuumlichtgeschwindigkeit und seine gemessene Geschwindigkeit ist 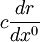$c\frac{dr}{dx^0}$. Sie stehen nach der obigen Definition der Eigenzeit in folgendem Zusammenhang

$c \frac{dr}{dx^0} = \sqrt{g_{00}(r)} \frac{dr}{d\tau} = \sqrt{\frac{g_{00}(r)}{-g_{11}(r)}} \frac{dx}{d\tau} \approx \frac{c}{1 - 2 \phi(x)}$

Wenn man beachtet, dass φ ein anziehendes Gravitationspotential, also negativ ist, erkennt man, dass die gemessene Geschwindigkeit des Lichtstrahls kleiner ist, als die Vakuumlichtgeschwindigkeit. Man kann also das Gravitationsfeld in dieser Betrachtung als Medium mit der ortsabhängigen Brechzahl 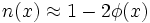$n(x) \approx 1 - 2 \phi(x)$ interpretieren. Da sich Licht entlang von Geodäten ausbreitet, lässt sich dies also auch so formulieren, dass nahe einer Masse die Geodäten im Raum gekrümmt sind. Neben der Lichtkrümmung führt dies auch zur Lichtverzögerung, die nach ihrem Entdecker als Shapiro-Verzögerung bezeichnet wird.

Am Sonnenrand ist φ = − 10 ^{− 6} woraus sich als Brechzahl n = 1,000.002 ergibt. Der Effekt ist also im Vergleich zur gewöhnlichen optischen Brechung sehr klein. Dementsprechend klein ist auch der Winkel der Lichtablenkung im Gravitationsfeld.

Experimentstatus

Die Lichtverzögerung wurde von Irwin I. Shapiro im Jahr 1964 theoretisch vorhergesagt^[1] und erstmals 1968^[2] und 1971^[3] gemessen. Hier wurde die Zeitverschiebung von an der Venus reflektierten Radarsignalen gemessen, während diese sich von der Erde aus hinter der Sonne befand, so dass die Radarwellen nahe am Sonnenrand passieren mussten. Die Genauigkeit der Messungen belief sich anfangs noch auf mehrere Prozent. Bei wiederholten Messungen und später auch durch Messungen mit Hilfe von Raumsonden (Mariner, Viking) anstelle der Venus konnte die Genauigkeit auf 0,1 % gesteigert werden.

Die bisher genaueste Messung des Effekts gelang 2002 bei der Konjunktion der Raumsonde Cassini mit der Sonne. Frequenzmessungen im Ka-Band ermöglichten die Bestimmung der Shapiro-Verzögerung mit einer Genauigkeit von 0,001%.^[4]

Einzelnachweise

1. ↑ Irwin I. Shapiro: Fourth Test of General Relativity in Physical Review Letters 13 (1964), 789 - 791 doi:10.1103/PhysRevLett.13.789
2. ↑ Irwin I. Shapiro et al.: Fourth Test of General Relativity: Preliminary Results. In: Physical Review Letters 20, 1968, S. 1265 - 1269
3. ↑ Irwin I. Shapiro et al.: Fourth Test of General Relativity: New Radar Result. In: Physical Review Letters 26, 1971, S. 1132 - 1135
4. ↑ B.Bertotti, L: Iess, P. Tortora, A test of general relativity using radio links with the Cassini spacecraft, Nature 425 (2003), 374–376 online

Literatur

• C. M. Will, Theory and experiment in gravitational physics, Cambridge University Press, Cambridge (1993). Standardwerk zur experiemtellen Überprüfung der ART
• C. M. Will, Was Einstein Right?: Putting General Relativity to the Test, Basic Books (1993). Eine populärwissenschaftliche Zusammenfassung desselben
• C. M. Will, The Confrontation between General Relativity and Experiment, Living Reviews in Relativity (2006). Kürzere, aber aktuellere Fassung von Theory and experiment in gravitational physics