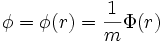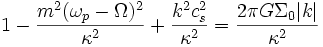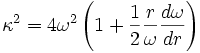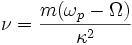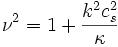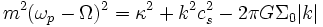- Lindblad-Resonanzen
-
Lindblad-Resonanzen sind ein Resonanzphänomen aus der Galaxientheorie.
Sie wurden von dem schwedischen Astronomen Bertil Lindblad entdeckt und sind nach ihm benannt. Die Dichtewellentheorie für Galaxien besagt: Die Spiralarme einer rotierenden Galaxie werden dadurch stabilisiert, dass im Gravitationsfeld der Galaxie mit konstanter Winkelgeschwindigkeit eine Welle umläuft. Die in dieser Theorie auftauchenden Resonanzen sollen nachfolgend erklärt werden.
Diese Resonanzen treten in der galaktischen Ebene auf, wenn die Bahnen der Sterne von einem winkelabhängigen Potential „gestört“ werden. Eine derartige winkelabhängige Störung kann etwa ein Spiralarm oder ein galaktischer Balken sein. Diese Störung rotiert mit der Winkelgeschwindigkeit
 , die im Allgemeinen nicht mit der Winkelgeschwindigkeit des restlichen Systems übereinstimmt.
, die im Allgemeinen nicht mit der Winkelgeschwindigkeit des restlichen Systems übereinstimmt.Es kommt zur Resonanz, wenn die Differenz zwischen der (Bahnradius-abhängigen) Winkelgeschwindigkeit der Sterne, ΩStern(R), und der Winkelgeschwindigkeit der Störung,
 , ein ganzzahliges Vielfaches der epizyklischen Frequenz κ ist:
, ein ganzzahliges Vielfaches der epizyklischen Frequenz κ ist:Die Radien, bei denen dieser Fall eintritt, heißen Lindblad-Resonanzen.
Ferner gibt es die sogenannte ko-rotierende Resonanz, die bei dem Radius auftritt, wo die Winkelgeschwindigkeit der Kreisbahnen der Sterne und die Winkelgeschwindigkeit der Störung identisch sind,
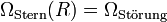 .
.Resonanzen
Wenn man davon ausgeht, daß die Dichteverteilung in einem System nicht stationär ist, so kann man deren Zeitentwicklung betrachten, indem man die Eulergleichung
mit einer Störung versieht. Dies bedeutet, daß für alle Variablen Σ, Φ, P und
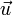 ein orts- und zeitabhängiger Störungsansatz gemacht wird. So wird z.B. die Dichte gemäß
ein orts- und zeitabhängiger Störungsansatz gemacht wird. So wird z.B. die Dichte gemäßgestört.
Eliminiert man dann in den aus dem Störungsansatz folgenden Gleichungen die ungestörten Anteile, so erhält man eine Poisson-Gleichung und drei Störungsgleichungen. Dieses Gleichungssystem wird durch einen Ansatz z.B. für die Dichte der Form
gelöst. Dieser Ansatz entspricht spiralförmigen Dichtewellen, mit m Armen, die mit der Frequenz ωp starr rotieren. In Ruhe folgt daraus für die Dichtemaxima das Muster
- mωpt0 − mφ + Φ(r) = 0
was für
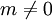 eine Spirale ist
eine Spirale istFindet man nun auch für die anderen Störungsgleichungen selbstkonsistente Lösungen, so erhält man ein algebraisches Gleichungssystem, das im weiteren dann auf eine Dispersionsrelation führt, die die Bedingung für eine spiralförmige Dichtewelle ausdrückt. Daraus wiederum folgt dann die Dispersionsgleichung
in der Ω für die Keplergeschwindigkeit steht,
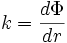 die radiale Wellenzahl ist und κ die Epizykelfrequenz, die definiert ist als
die radiale Wellenzahl ist und κ die Epizykelfrequenz, die definiert ist alsIn der o.a. Dispersionsgleichung ist ωp ein freier Parameter. Führt man nun eine Variable
ein, so erhält man aus
zwei Resonanzen. Formt man die Dispersionsgleichung um zu
so erkennt man, die Resonanzen als
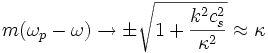 für
für 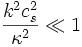
Diese Resonanzen heißen innere (-) und äußere (+) Lindblad-Resonanzen. Für ein gegebenes Modell lassen sich entsprechende Radien berechnen.
Quellen
Diplomarbeit „Superhumps hinter Gittern - was Euler zu Superhumps sagt“ mit Referenzen.
Wikimedia Foundation.

![m\left[ \Omega_\text{Stern}(R) - \Omega_\mathrm{St\ddot orung}\right] = \pm\kappa \qquad\text{mit}\qquad m\in\mathbb{N}](/pictures/dewiki/50/2e4d4a87e5c8403d317b403670d866bb.png)
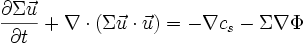
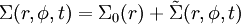
![\tilde{\Sigma}(r,\phi,t) = \tilde{\Sigma}^*(r)\exp\left(i[m\omega_p t - m\phi + \Phi(r)]\right)](/pictures/dewiki/53/589f1e84f590264c2320c643516a8520.png)