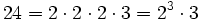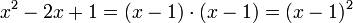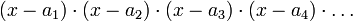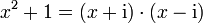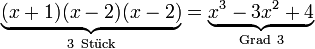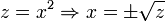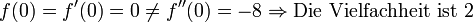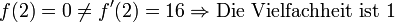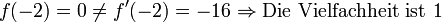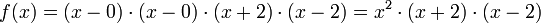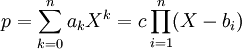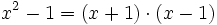Linearfaktor

Als Faktorisierung von Polynomen in der Algebra versteht man analog zur Primfaktorzerlegung von ganzen Zahlen das Zerlegen von Polynomen in Faktoren.

Erklärung

Jede ganze Zahl lässt sich eindeutig in Primfaktoren zerlegen:

$24 = 2 \cdot 2 \cdot 2 \cdot 3 = 2^3 \cdot 3$

Ähnlich lassen sich Polynome in Faktoren zerlegen:

$x^2 - 2x + 1 = (x-1) \cdot (x-1) = (x-1)^2$

Eine Faktorisierung hat immer die Form:

$(x - a_1) \cdot (x-a_2) \cdot (x-a_3) \cdot (x-a_4) \cdot \dots$

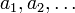Wobei $a_1, a_2, \dots$ die Nullstellen des Polynoms sind. Doch Vorsicht! Manche Nullstellen kommen mehrfach vor, deswegen kann man nicht einfach nur die Nullstellen bestimmen: Von x² ist 0 die einzige Nullstelle, daraus könnte man folgern, die Faktorisierung ist x, sie ist jedoch $x \cdot x$.

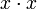Falls das Polynom komplexe Nullstellen besitzt, enthält die Faktorisierung komplexe Zahlen:

$x^2 + 1 = (x + \mathrm{i}) \cdot (x - \mathrm{i})$

Bei einem Polynom mit reellen Koeffizienten ist aber immer mit einer komplexen Zahl z auch deren konjugiert komplexe 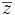$\overline z$ Nullstelle. Das Polynom hat dann eine Faktorisierung

$(x - a_1) \cdot (x-a_2) \cdot (x-a_3) \cdot (x-a_4) \cdot \dots \cdot (x^2+b_1x+c_1)\cdot (x^2+b_2x+c_2)\cdot (x^2+b_3x+c_3)\cdot \dots$,

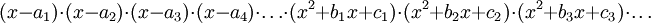wobei zu den quadratischen Formen (x² + bx + c) die Nullstellen z, 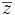$\overline z$ gehören.

Die Anzahl der Faktoren entspricht dem Grad des Polynoms:

$\underbrace{(x+1)(x-2)(x-2)}_{\mathrm{3~St\ddot uck}} = \underbrace{x^3 - 3x^2 + 4}_{\mathrm{Grad~3}}$

Oben wurde gesagt, dass die Anzahl der Nullstellen nicht unbedingt der Anzahl der Faktoren entspricht. Es gilt jedoch: Die Anzahl der Faktoren entspricht der Anzahl der Nullstellen mal der entsprechenden Vielfachheiten bzw. Ordnungen. So lässt sich die Faktorisierung bestimmen:

Beispiel

f(x) = x⁴ − 4x²

Über Substitution mit z = x²:

f(x) = z² − 4z

Die Nullstellen sind: z₁ = 0 und z₂ = 4. Rücksubstitution:

$z = x^2 \Rightarrow x = \pm \sqrt{z}$

Die Nullstellen sind 0, 2 und -2. Die Vielfachheiten lassen sich über die Ableitungen bestimmen:

f'(x) = 4x³ − 8x

f''(x) = 12x² − 8

f'''(x) = 24x

f''''(x) = 24

Nun ist:

$f(0) = f'(0) = 0 \ne f''(0) = -8 \Rightarrow \mbox{Die Vielfachheit ist 2}$

$f(2) = 0 \ne f'(2) = 16 \Rightarrow \mbox{Die Vielfachheit ist 1}$

$f(-2) = 0 \ne f'(-2) = -16 \Rightarrow \mbox{Die Vielfachheit ist 1}$

Die Faktorisierung ist nun:

$f(x) = (x - 0) \cdot (x - 0) \cdot (x + 2) \cdot (x - 2) = x^2 \cdot (x+2) \cdot (x-2)$

Mathematische Beschreibung

Dabei versucht man, für ein gegebenes Polynom p aus einem Polynomring R eine endliche Menge 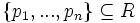$\lbrace p_1, ..., p_n \rbrace \subseteq R$ zu finden, sodass $p = \prod_{i=1}^n p_i$.

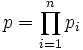In einem faktoriellen Ring existiert dabei ein Primsystem, sodass diese Darstellung bis auf die Reihenfolge und Assoziiertheit eindeutig ist und jedes p_i ein Element des Primsystems ist. In Ringen, die nicht faktoriell sind, ist es im Allgemeinen nicht möglich, eine eindeutige Faktorisierung zu finden.

Über dem Körper der komplexen Zahlen $\mathbb{C}$ lässt sich jedes Polynom n-ten Grades als Produkt von genau n Linearfaktoren X − b_i

$p = \sum_{k=0}^n a_k X^k = c \prod_{i=1}^n (X - b_i)$

schreiben. Dies ist eine der Aussagen des Fundamentalsatzes der Algebra. Man sagt, das Polynom zerfällt in seine Linearfaktoren. Die b_i sind genau die Nullstellen der zugehörigen Polynomfunktion. Hinzu kommt ein Faktor c, da Vielfache eines Polynoms dieselben Nullstellen haben.

Die algebraisch abgeschlossenen komplexen Zahlen sind eine Körpererweiterung der Dimension 2 über den reellen Zahlen. Daher lassen sich Polynome aus $\mathbb{R}[X]$ (der Polynomring über den reellen Zahlen) als Produkt von quadratischen und linearen Faktoren darstellen.

Beispiele

• Das Polynom x² − 1 hat die Nullstellen 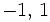$-1,\, 1$ und damit die Faktorisierung

  $x^2 - 1 = (x+1)\cdot(x-1)$

• Das Polynom x² + 1 hat die komplexen Nullstellen 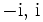$-\mathrm{i},\,\mathrm{i}$ und damit die Faktorisierung

  $x^2 + 1 = (x+\mathrm{i})\cdot(x-\mathrm{i})$

Algorithmen

Elwyn Ralph Berlekamp veröffentlichte 1967 den Berlekamp-Algorithmus, mit dem Polynome über dem Restklassenkörper 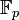$\mathbb{F}_p$ faktorisiert werden können.