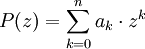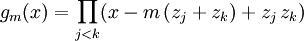- Fsda
-
Der (gaußsche) Fundamentalsatz der Algebra besagt, dass der Körper
 der komplexen Zahlen algebraisch abgeschlossen ist.
der komplexen Zahlen algebraisch abgeschlossen ist.Das bedeutet anders ausgedrückt: Sucht man Nullstellen eines nicht konstanten Polynoms mit ganzen, reellen oder komplexen Koeffizienten, und dehnt man die Suche in den Bereich der komplexen Zahlen aus, so wird man immer fündig.
Inhaltsverzeichnis
Satz
Sei
ein nicht konstantes Polynom vom Grad
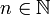 ,
, 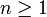 , mit komplexen Koeffizienten
, mit komplexen Koeffizienten 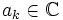 . Dann hat das Polynom eine komplexe Nullstelle, d. h. es gibt eine Zahl
. Dann hat das Polynom eine komplexe Nullstelle, d. h. es gibt eine Zahl 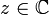 , so dass P(z) = 0 gilt. Genauer gilt sogar, dass die Anzahl der Nullstellen, wenn sie mit der richtigen Vielfachheit gezählt werden, insgesamt gleich dem Grad des Polynoms ist.
, so dass P(z) = 0 gilt. Genauer gilt sogar, dass die Anzahl der Nullstellen, wenn sie mit der richtigen Vielfachheit gezählt werden, insgesamt gleich dem Grad des Polynoms ist.Beispiel
Die Polynomgleichung
- P(x) = x5 − 5x4 + 17x3 − 13x2 = 0
hat die Lösungen
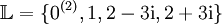 ,
,
die natürlich die Nullstellen des Polynomes sind. Die Lösung 0 wird dabei doppelt gezählt, wie anhand der Faktorisierung des Polynoms ersichtlich ist:
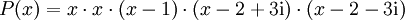 .
.
Man verwendet auch die Sprechweise „0 tritt mit Vielfachheit 2 auf“, alle anderen Nullstellen treten mit Vielfachheit 1 auf. Dieses Beispiel zeigt auch, dass die Nullstellen im Allgemeinen nicht (alle) reell sind, selbst wenn das Polynom reelle Koeffizienten hat.
Anmerkungen
Von einem Polynom f(z) lässt sich der zu einer Nullstelle z0 mit f(z0) = 0 gehörende Linearfaktor (z − z0) abspalten. (Dazu kann beispielsweise die Horner-Ruffini-Methode verwendet werden.) Durch die Abspaltung ergibt sich ein im Grad um Eins reduziertes Polynom, für das man das Verfahren wiederholen kann. Deshalb zerfällt jedes nicht konstante Polynom über
 komplett in ein Produkt aus Linearfaktoren:
komplett in ein Produkt aus Linearfaktoren: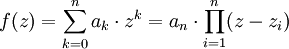 ,
,
wobei die zi die Nullstellen des Polynoms sind.
Bei Polynomen mit reellen Koeffizienten ist die konjugierte Zahl einer Nullstelle wieder eine Nullstelle. Das heißt, ist λ = x + iy eine Nullstelle, so auch
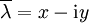 .
.Beweis: Mit
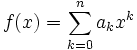 und f(λ) = 0 ist
und f(λ) = 0 ist 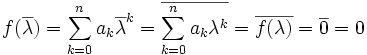 .
.Daraus folgt, dass nicht-reelle Nullstellen bei Polynomen mit reellen Koeffizienten immer paarweise auftreten, das heißt, die Anzahl der komplexen (nicht reellen) Nullstellen ist gerade. Daraus kann man auch folgern, dass jedes Polynom mit reellen Koeffizienten und ungeradem Grad eine reelle Nullstelle hat. Aber das folgt schon ganz elementar aus dem Zwischenwertsatz.
Beweise
Erste Formulierungen des Fundamentalsatzes finden sich im 17. Jahrhundert (Peter Roth, Albert Girard, René Descartes). Der erste veröffentlichte Beweis von Jean d'Alembert 1746 war von der Idee her korrekt, jedoch enthielt er Lücken, die erst mit den Methoden der Analysis des 19. Jahrhunderts geschlossen werden konnten. Eine vereinfachte und auch nach modernen Kriterien noch korrekte Version dieses Beweises wurde von Jean-Robert Argand 1806 angegeben.
Der erste vollständige Beweis für den Fundamentalsatz der Algebra wurde 1799 von Carl Friedrich Gauß im Rahmen seiner Dissertation angegeben. Auch dieser Beweis enthält einige analytische Schwächen, die erst später beseitigt werden konnten. Der zweite Beweis, der von Gauß 1815 vorgestellt und ein Jahr später publiziert wurde, baut auf Ideen von Leonhard Euler auf und benutzt als analytische Grundlage, unbewiesen und ohne dass eine Beweisnotwendigkeit gesehen wurde, lediglich den Zwischenwertsatz der reellen Analysis.
Ein Beweis, der gleichzeitig ein effizientes Berechnungsverfahren beinhaltet, wurde 1859 (und nochmals 1891) von Karl Weierstraß veröffentlicht. Das darin enthaltene Verfahren wird heute als Weierstraß-(Durand-Kerner)-Verfahren bezeichnet.
Inzwischen kennt man mehrere sehr unterschiedliche Beweise, die Begriffe und Ideen aus Analysis, Algebra oder Topologie beinhalten. Trotz seines Namens kann der Satz nicht mit rein algebraischen Methoden bewiesen werden, da er eine Aussage über den Körper
 macht – und dieser ist ein Konstrukt der Analysis. Am kürzesten kann der Fundamentalsatz der Algebra nach Cauchy und Liouville mit Methoden der Funktionentheorie bewiesen werden.
macht – und dieser ist ein Konstrukt der Analysis. Am kürzesten kann der Fundamentalsatz der Algebra nach Cauchy und Liouville mit Methoden der Funktionentheorie bewiesen werden.Im folgenden sei
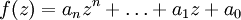 stets ein Polynom mit komplexen Koeffizienten und insbesondere
stets ein Polynom mit komplexen Koeffizienten und insbesondere  . Dieses sei als Funktion
. Dieses sei als Funktion  aufgefasst.
aufgefasst.Rein analytischer Beweis
Dieser Beweis wurde 1746 von d'Alembert vorgeschlagen, jedoch erst 1806 von J.-R. Argand vervollständigt. Die zentrale Aussage dieses Beweises ist, dass zu jedem Punkt
 , der keine Nullstelle ist, ein Punkt z+w in der Umgebung angegeben werden kann, dessen Funktionswert einen kleineren Betrag hat, | f(z + w) | < | f(z) | . Hat der Betrag der Funktionswerte also einen Minimalpunkt, so muss dieser ein Nullpunkt sein. Da die Menge
, der keine Nullstelle ist, ein Punkt z+w in der Umgebung angegeben werden kann, dessen Funktionswert einen kleineren Betrag hat, | f(z + w) | < | f(z) | . Hat der Betrag der Funktionswerte also einen Minimalpunkt, so muss dieser ein Nullpunkt sein. Da die Menge 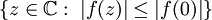 kompakt ist, und der Betrag verknüpft mit f stetig, gibt es immer einen solchen Minimalpunkt und damit eine Nullstelle.
kompakt ist, und der Betrag verknüpft mit f stetig, gibt es immer einen solchen Minimalpunkt und damit eine Nullstelle.Zur zentralen Aussage entwickle man f in z, d. h.
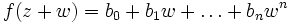 . Ist b0 = 0, so ist z eine Nullstelle. Sonst wähle dasjenige k>0, für welches als erstes
. Ist b0 = 0, so ist z eine Nullstelle. Sonst wähle dasjenige k>0, für welches als erstes 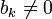 gilt und betrachte die beiden Ungleichungen für
gilt und betrachte die beiden Ungleichungen für 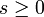
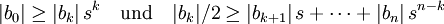 .
.
Beide Ungleichungen sind für s=0 erfüllt und es gibt ein endliches größtes s, so dass sie erfüllt sind. Für dieses wähle ein
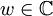 mit | w | = s und so, dass mit einem reellen Faktor 1>c>0 die Beziehnung
mit | w | = s und so, dass mit einem reellen Faktor 1>c>0 die Beziehnung 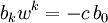 gilt. Für den interessierenden Betrag des Funktionswertes gilt nun nach Dreiecksungleichung
gilt. Für den interessierenden Betrag des Funktionswertes gilt nun nach Dreiecksungleichung![\begin{array}{rlrl}
|f(z+w)|\le&amp;|b_0+b_kw^k|+\sum_{j&gt;k}|b_j|\,|w|^j&amp;
=&amp;(1-c)|b_0|+\sum_{j&gt;k}|b_j|\,s^j\\[.3em]
=&amp;|b_0|-s^k\left(|b_k|-\sum_{j&gt;k}|b_j|\,s^{j-k}\right)&amp;
\le&amp; |f(z)|-\tfrac12\,|b_k|\,s^k
\end{array}](/pictures/dewiki/101/ea2704bf43402dfa4d5a1e3c80550057.png) .
.
Beweis mit Methoden der Topologie
Ein Beweis mit dieser Methode wurde 1799 von Gauß gegeben. Er zerlegte die Polynomfunktion in Real- und Imaginärteil, f(x + iy) = u(x,y) + iv(x,y). Die Nullstellenmengen von u und v sind aus einzelnen eindimensionalen Bögen zusammengesetzt, die eine endliche Anzahl von Knotenpunkten in der Ebene verbinden. Von jedem Knotenpunkt geht eine gerade Anzahl von Bögen aus. Auf keinen Fall kann ein Bogen in einem Punkt einfach enden. Auf jedem Kreis mit genügend großem Radius gibt es 2n Nullstellen von u und 2n Nullstellen von v, die sich abwechseln. Jeder zusammenhängende Teil des Nullstellengraphen von u hat auf einem großen Kreis eine gerade Anzahl von Schnittstellen, die eine ungerade Anzahl von Schnittstellen des Nullstellengraphen von v einschließen. Damit muss ein Bogen des Graphen von v aus dem zusammenhängenden Teilstück des Graphen von u herausragen. Dies geht nur, wenn die Graphen von u und v sich schneiden, der Schnittpunkt aber ist eine Nullstelle von f(z).
Moderne Versionen dieses Beweises benutzen den Begriff der Windungszahl. Es sei angenommen, dass das Polynom f(z) keine komplexen Nullstellen besitze. Dann kann für jedes s>0 eine geschlossene, stetige Kurve
![\gamma_s:[0,2\pi]\to\mathbb C](/pictures/dewiki/100/d83b8ebbbb34b26256fa639f96679e33.png) ,
, 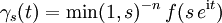
konstruiert werden, die die (skalierten) Funktionswerte des Polynoms auf dem Kreis mit Radius s durchläuft. Da kein Funktionswert Null ist, kann eine Windungszahl definiert werden. Da sich die Kurve bei Änderung des Parameters s stetig ändert, kann sich die Windungszahl nur ändern, wenn die sich ändernde Kurve den Nullpunkt überquert. Da nach Annahme die Funktion f(z) keine Nullstelle besitzt, ist eine solche Überquerung des Nullpunktes nicht möglich. Daher muss die Windungszahl für alle s>0 dieselbe sein.
Für sehr große Werte von s wird die Kurve der entsprechenden Kurve der n-ten Potenz, genauer des Polynoms anzn, immer ähnlicher, die Windungszahl muss daher konstant n sein. Für sehr kleine Werte von s wird die Kurve der konstanten Kurve mit Wert a0 immer ähnlicher, also muss die – für alle s>0 konstante – Windungszahl gleichzeitig den Wert 0 besitzen. Dies ist gleichzeitig nur möglich, wenn n=0 gilt, das Polynom also konstant ist. Für Polynome höheren Grades führt dieses Argument zum Widerspruch, also muss es Nullstellen z mit f(z)=0 geben.
Beweis mit dem Zwischenwertsatz und algebraischen Methoden
Ein solcher Beweis wurde 1815 von Gauß präsentiert. Es wird benutzt, dass nach dem Zwischenwertsatz jedes reelle Polynom ungeraden Grades mindestens eine Nullstelle hat, sowie dass quadratische Gleichungen, auch mit komplexen Koeffizienten, elementar lösbar sind. Der Beweis erfolgt als vollständige Induktion über die Potenz des Faktors 2 im Grad des Polynoms.
Es sei zunächst f(z) quadratfrei und mit reellen Koeffizienten vorausgesetzt. Der Grad habe eine Faktorisierung
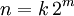 mit k ungerade. Der Beweis erfolgt als vollständige Induktion über die Potenz m des Faktors 2 im Grad des Polynoms. Ist m=0, so gibt es eine Nullstelle nach dem Zwischenwertsatz. Es sei nun im Induktionsschritt vorausgesetzt, dass alle Polynome mit Graden
mit k ungerade. Der Beweis erfolgt als vollständige Induktion über die Potenz m des Faktors 2 im Grad des Polynoms. Ist m=0, so gibt es eine Nullstelle nach dem Zwischenwertsatz. Es sei nun im Induktionsschritt vorausgesetzt, dass alle Polynome mit Graden 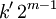 mit k' ungerade mindestens eine Nullstelle besitzen.
mit k' ungerade mindestens eine Nullstelle besitzen.Es sei, der Einfachheit halber, ein (abstrakter) Zerfällungskörper
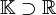 des Polynoms f(z) konstruiert, in welchem es die paarweise verschiedenen (wiederum abstrakten) Nullstellen
des Polynoms f(z) konstruiert, in welchem es die paarweise verschiedenen (wiederum abstrakten) Nullstellen 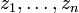 hat,
hat,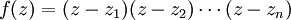 .
.
In
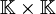 sei die Menge der
sei die Menge der 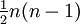 Punkte
Punkte 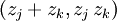 , j<k, betrachtet. Da die abstrakten Nullstellen paarweise verschieden sind, gibt nur eine endliche Anzahl von Geraden, die durch mindestens zwei dieser Punkte verlaufen, insbesondere auch nur eine endliche Anzahl reeller Anstiege m solcher Geraden, für welche die Differenz
, j<k, betrachtet. Da die abstrakten Nullstellen paarweise verschieden sind, gibt nur eine endliche Anzahl von Geraden, die durch mindestens zwei dieser Punkte verlaufen, insbesondere auch nur eine endliche Anzahl reeller Anstiege m solcher Geraden, für welche die Differenz 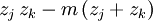 zweimal denselben Wert annimmt. Für alle anderen Werte von m ist das Polynom
zweimal denselben Wert annimmt. Für alle anderen Werte von m ist das Polynomebenfalls quadratfrei und symmetrisch in den abstrakten Nullstellen
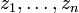 . Daher können die Koeffizienten von gm(x) als Polynome in m und den Koeffizienten von f(z) dargestellt werden, gm(x) ist also für jedes reelle m ein Polynom mit reellen Koeffizienten und kann mittels Resultanten aus f(z) bestimmt werden. Der Grad von gm(x) beträgt
. Daher können die Koeffizienten von gm(x) als Polynome in m und den Koeffizienten von f(z) dargestellt werden, gm(x) ist also für jedes reelle m ein Polynom mit reellen Koeffizienten und kann mittels Resultanten aus f(z) bestimmt werden. Der Grad von gm(x) beträgt 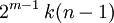 , wobei k(n-1) eine ungerade Zahl ist. Nach Induktionsvoraussetzung gibt es wenigstens eine komplexe Nullstelle x mit gm(x) = 0. Aus den partiellen Ableitungen nach m und x in der Nullstelle können komplexe Zahlen p und q bestimmt werden, so dass mindestens eine der Nullstellen von
, wobei k(n-1) eine ungerade Zahl ist. Nach Induktionsvoraussetzung gibt es wenigstens eine komplexe Nullstelle x mit gm(x) = 0. Aus den partiellen Ableitungen nach m und x in der Nullstelle können komplexe Zahlen p und q bestimmt werden, so dass mindestens eine der Nullstellen von 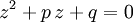 eine Nullstelle von f(z) ist.
eine Nullstelle von f(z) ist.Hat f(z) auch echt komplexe Koeffizienten, so hat
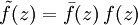 nur reelle Koeffizienten. Jede Nullstelle des Produkts ist Nullstelle eines Faktors, somit also selbst oder als komplex konjugierte Zahl eine Nullstelle von f(z). Ist das nun reelle Polynom nicht quadratfrei, so kann mit Polynomarithmetik (u.a. euklidischer Algorithmus) eine Faktorisierung in (nichtkonstante) quadratfreie Faktoren gefunden werden, von denen jeder mindestens eine Nullstelle enthält.
nur reelle Koeffizienten. Jede Nullstelle des Produkts ist Nullstelle eines Faktors, somit also selbst oder als komplex konjugierte Zahl eine Nullstelle von f(z). Ist das nun reelle Polynom nicht quadratfrei, so kann mit Polynomarithmetik (u.a. euklidischer Algorithmus) eine Faktorisierung in (nichtkonstante) quadratfreie Faktoren gefunden werden, von denen jeder mindestens eine Nullstelle enthält.Beweis mit Methoden der Funktionentheorie
Wegen
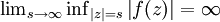 existiert ein R > 0,so dass
existiert ein R > 0,so dass 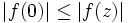 für alle
für alle 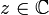 mit | z | > R gilt. Weil sowohl f und damit auch der Betrag | f | stetig sind, als auch die Kreisscheibe
mit | z | > R gilt. Weil sowohl f und damit auch der Betrag | f | stetig sind, als auch die Kreisscheibe 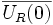 kompakt ist, existiert nach dem Satz von Weierstrass eine Stelle
kompakt ist, existiert nach dem Satz von Weierstrass eine Stelle 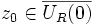 mit minimalem Betrag des Funktionswertes,
mit minimalem Betrag des Funktionswertes, 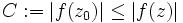 für alle
für alle 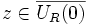 . Nach Konstruktion ist
. Nach Konstruktion ist 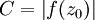 sogar ein globales Minimum. Wäre C positiv, so wäre die reziproke Funktion
sogar ein globales Minimum. Wäre C positiv, so wäre die reziproke Funktion 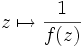 holomorph auf
holomorph auf  und durch
und durch 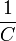 beschränkt, also nach dem Satz von Liouville konstant. Somit wäre auch f(z) konstant, was der Voraussetzung widerspricht. Es gibt also eine Nullstelle (in z0).
beschränkt, also nach dem Satz von Liouville konstant. Somit wäre auch f(z) konstant, was der Voraussetzung widerspricht. Es gibt also eine Nullstelle (in z0).Beweis mit Methoden der komplexen Geometrie
Wir fassen f(z) als Abbildung des komplex-projektiven Raums
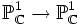 auf, d. h.
auf, d. h. 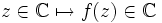 ,
, 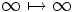 . Die so definierte Abbildung komplexer Mannigfaltigkeiten ist holomorph und damit offen (d. h. das Bild jeder offenen Teilmenge ist offen). Da
. Die so definierte Abbildung komplexer Mannigfaltigkeiten ist holomorph und damit offen (d. h. das Bild jeder offenen Teilmenge ist offen). Da 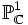 kompakt und f stetig ist, ist das Bild
kompakt und f stetig ist, ist das Bild 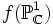 auch kompakt, insbesondere abgeschlossen in
auch kompakt, insbesondere abgeschlossen in 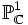 . Damit ist das Bild bereits ganz
. Damit ist das Bild bereits ganz 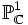 , denn
, denn 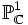 ist zusammenhängend. Insbesondere gibt es ein
ist zusammenhängend. Insbesondere gibt es ein 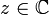 , welches auf 0 abgebildet wird, d. h. eine Nullstelle von f.
, welches auf 0 abgebildet wird, d. h. eine Nullstelle von f.Einzelnachweise
Literatur
- C. F. Gauss: Another new proof of the theorem that every integral rational algebraic function of one variable can be resolved into real factors of the first or second degree, 1815 (engl. Übersetzung des Originals in Latein).
- Weierstraß, Karl (1891). Neuer Beweis des Satzes, dass jede ganze rationale Function einer Veränderlichen dargestellt werden kann als ein Product aus linearen Functionen derselben Veränderlichen. Sitzungsberichte der königlich preussischen Akademie der Wissenschaften zu Berlin.
- S. Basu, R. Pollack, M.-F. Roy: Algorithms in Real Algebraic Geometry. 2. Auflage. Springer 2006, ISBN 978-3-540-33098-1.
Wikimedia Foundation.