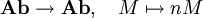Exakter Funktor — ist ein mathematischer Begriff aus der Kategorientheorie. Ein linksexakter bzw. rechtsexakter Funktor ist ein additiver Funktor zwischen additiven Kategorien, der Kerne bzw. Kokerne erhält. Ein exakter Funktor ist ein Funktor, der sowohl links… … Deutsch Wikipedia
Linksexakter Funktor — Exakter Funktor ist ein mathematischer Begriff aus der Kategorientheorie. Ein linksexakter bzw. rechtsexakter Funktor ist ein additiver Funktor zwischen additiven Kategorien, der Kerne bzw. Kokerne erhält. Ein exakter Funktor ist ein Funktor, der … Deutsch Wikipedia
Rechtsexakt — Exakter Funktor ist ein mathematischer Begriff aus der Kategorientheorie. Ein linksexakter bzw. rechtsexakter Funktor ist ein additiver Funktor zwischen additiven Kategorien, der Kerne bzw. Kokerne erhält. Ein exakter Funktor ist ein Funktor, der … Deutsch Wikipedia
Rechtsexakter Funktor — Exakter Funktor ist ein mathematischer Begriff aus der Kategorientheorie. Ein linksexakter bzw. rechtsexakter Funktor ist ein additiver Funktor zwischen additiven Kategorien, der Kerne bzw. Kokerne erhält. Ein exakter Funktor ist ein Funktor, der … Deutsch Wikipedia
Adjungierter Funktor — Adjungiert heißen zwei Funktoren F: C → D, G: D → C zwischen zwei Kategorien C und D, die gewissermaßen ein Ersatz für eine fehlende Äquivalenz von Kategorien sind. Inhaltsverzeichnis 1 Definition 2 Einheit und Koeinheit der Adjunktion 3… … Deutsch Wikipedia
Linksadjungiert — Adjungiert heißen zwei Funktoren F: C → D, G: D → C zwischen zwei Kategorien C und D, die gewissermaßen ein Ersatz für eine fehlende Äquivalenz von Kategorien sind. Inhaltsverzeichnis 1 Definition 2 Einheit und Koeinheit der Adjunktion 3… … Deutsch Wikipedia
Rechtsadjungiert — Adjungiert heißen zwei Funktoren F: C → D, G: D → C zwischen zwei Kategorien C und D, die gewissermaßen ein Ersatz für eine fehlende Äquivalenz von Kategorien sind. Inhaltsverzeichnis 1 Definition 2 Einheit und Koeinheit der Adjunktion 3… … Deutsch Wikipedia
Torsionsfrei — Torsion ist das Phänomen der kommutativen Algebra, also der Theorie der Moduln über kommutativen Ringen, das sie fundamental von der (einfacheren) Theorie der Vektorräume unterscheidet. Torsion ist verwandt mit dem Begriff des Nullteilers.… … Deutsch Wikipedia
Torsionsgruppe — Torsion ist das Phänomen der kommutativen Algebra, also der Theorie der Moduln über kommutativen Ringen, das sie fundamental von der (einfacheren) Theorie der Vektorräume unterscheidet. Torsion ist verwandt mit dem Begriff des Nullteilers.… … Deutsch Wikipedia
Torsionsuntergruppe — Torsion ist das Phänomen der kommutativen Algebra, also der Theorie der Moduln über kommutativen Ringen, das sie fundamental von der (einfacheren) Theorie der Vektorräume unterscheidet. Torsion ist verwandt mit dem Begriff des Nullteilers.… … Deutsch Wikipedia