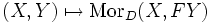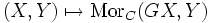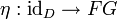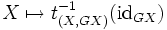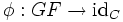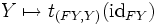Rechtsadjungiert

Adjungiert heißen zwei Funktoren F: C → D, G: D → C zwischen zwei Kategorien C und D, die gewissermaßen ein Ersatz für eine fehlende Äquivalenz von Kategorien sind.

Definition

Zwei Funktoren 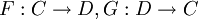$F:C\to D,G:D\to C$ zwischen zwei Kategorien C und D bilden ein Paar adjungierter Funktoren, wenn die Funktoren

$(X,Y)\mapsto\operatorname{Mor}_D(X,FY)$

und

$(X,Y)\mapsto\operatorname{Mor}_C(GX,Y)$

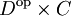von $D^\operatorname{op}\times C$ nach Set natürlich äquivalent sind. (Die natürliche Äquivalenz ist Bestandteil der Struktur "adjungiertes Funktorpaar".)

F heißt rechtsadjungiert zu G, G heißt linksadjungiert zu F.

Einheit und Koeinheit der Adjunktion

Ist t die natürliche Äquivalenz 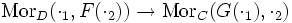$\operatorname{Mor}_D(\cdot_1,F(\cdot_2))\to \operatorname{Mor}_C(G(\cdot_1),\cdot_2)$, so heißen die natürlichen Transformationen

$\eta:\operatorname{id}_D\to FG$

$X\mapsto t_{(X,GX)}^{-1}(\operatorname{id}_{GX})$

und

$\phi:GF\to\operatorname{id}_C$

$Y\mapsto t_{(FY,Y)}(\operatorname{id}_{FY})$

Einheit bzw. Koeinheit der Adjunktion.

Einheit und Koeinheit haben die Eigenschaft, dass die beiden induzierten Transformationen

F → FGF → F

und

G → GFG → G

die Identität ergeben. Umgekehrt kann man zeigen, dass zwei derartige natürliche Transformationen eine Adjunktion bestimmen.

Eigenschaften

• Sind F und G quasi-invers zueinander, so ist F rechts- und linksadjungiert zu G.
• Rechtsadjungierte Funktoren erhalten Limites (sind also linksexakt), linksadjungierte Funktoren erhalten Kolimites (sie sind rechtsexakt).

Beispiele

• Der Funktor "freie abelsche Gruppe über einer Menge" ist linksadjungiert zum Vergissfunktor Ab → Set.
• Der Funktor "statte eine Menge mit der diskreten Topologie aus" ist linksadjungiert zum Vergissfunktor Top → Set.
• Der Funktor "disjunkte Vereinigung mit einem einpunktigen Raum" ist linksadjungiert zum Vergissfunktor Top^* → Top.
• Der Funktor "Stone-Čech-Kompaktifizierung" ist linksadjungiert zum Vergissfunktor von der Kategorie der kompakten Hausdorffräume in die Kategorie aller topologischer Räume.
• Der Funktor "Vervollständigung" ist linksadjungiert zum Vergissfunktor von der Kategorie der vollständigen metrischen Räume in die Kategorie aller metrischen Räume.
• Die reduzierte Einhängung ist linksadjungiert zum Schleifenraum; beide Kategorien sind dabei die punktierten topologischen Räume mit den Homotopieklassen von punktierten Abbildungen als Morphismen.