- Logarithmentabelle
-
Logarithmentafel nennt man eine tabellarische Darstellung der Mantissen der Logarithmen (meist zur Basis 10) der Zahlen, in der Regel von 1,00 bis 9,99. Logarithmentafeln waren über Jahrhunderte ein wichtiges Rechenhilfsmittel, besonders im natur- und ingenieurwissenschaftlichen Bereich. Viele Berechnungen in der Schulmathematik, z. B. das Ziehen von schwierigen Wurzeln, konnten nur mit ihrer Hilfe durchgeführt werden. Die Erfindung und weite Verbreitung von Taschenrechnern und Computern hat die Verwendung von Logarithmentafeln, ähnlich wie die von Rechenschiebern, innerhalb weniger Jahre praktisch völlig überflüssig gemacht.
Inhaltsverzeichnis
Geschichte
Als Erfinder der Logarithmentafeln gilt John Napier, der sie in seinem Werk Mirifici Logarithmorum Canonis Descriptio 1614 veröffentlichte. Unabhängig von Napier entwickelte auch der Schweizer Jost Bürgi in Kassel eine Logarithmentafel. Als Mitarbeiter von Johannes Kepler verwendete er die selbst erstellten Logarithmentafeln für seine Berechnungen für Kepler. Henry Briggs entwickelte die Logarithmentafeln dahingehend weiter, dass er sie zur Basis 10 erstellte. Hier waren die Logarithmen der Zahlen von 1 bis 20.000 und von 90.000 bis 100.000 auf 14 Stellen genau aufgeführt.
Gebrauch von Logarithmentafeln
Logarithmentafeln erlauben es, die Multiplikation und Division von Zahlen auf die einfachere Addition und Subtraktion zurückzuführen. Bevor es mechanische oder elektrische Rechenmaschinen gab, erleichterten Logarithmentafeln das Rechnen ungemein. So waren Logarithmentafeln in der Schule unter anderem im Mathematik- und Physikunterricht der Oberstufe unverzichtbare Begleiter.
Das Produkt zweier Zahlen, a und b, wird aufgrund
dadurch berechnet, dass der Logarithmus der Zahl a zur Basis x und derjenige der Zahl b zur Basis x in der Tabelle nachgeschlagen wird. Die Summe der beiden Logarithmen wird gebildet, und in der Tabelle gesucht. Die diese Summe als Logarithmus ergebende Zahl ist dann das Produkt von a und b.
So lassen sich mit Hilfe einer Logarithmentafel weitere Rechenarten auf eine einfachere Addition bzw. Subtraktion, in manchen Fällen auch auf eine Multiplikation bzw. Addition zurückführen. Diese Rückführungen beruhen dabei auf den Logarithmengesetzen:
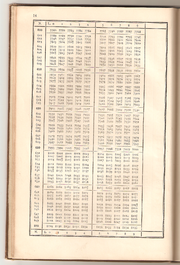
Aufbau einer Logarithmentafel
Am verbreitetsten waren drei-, vier- und fünfstellige Logarithmentafeln. Je größer die Genauigkeit einer Tafel sein soll, desto mehr wächst ihr Umfang. In der Schule waren bis in die 1970er Jahre des 20. Jahrhunderts gewöhnlich vierstellige Logarithmentafeln im Gebrauch.
Einfache dreistellige Logarithmentafeln sind so aufgebaut, dass die ersten beiden Ziffern (also 10 bis 99) den linken Tabellenrand bilden, während die dritte Ziffer (0 bis 9) als Spaltenüberschrift dient.
Der Zahlenbereich von 1,00 bis 9,99 genügt, da sich zur Basis 10 daraus der Logarithmus jeder anderen Zahl leicht erzeugen lässt, verändert wird lediglich der Teil vor dem Komma. Beispiel: Der Logarithmus von 2 ist 0,30103; der Logarithmus von 20 ist 1,30103 und der Logarithmus von 200 ist 2,30103 usw.
Logarithmen zu Zahlen mit vier aktiven Stellen lassen sich durch lineare Interpolation ermitteln.
Erzeugen einer Logarithmentafel
Im Folgenden wird beschrieben, wie man sich Logarithmen zur Basis 10 (oder jeder beliebigen anderen Basis) ohne Taschenrechner selbst erzeugen kann und wie dies auch historisch gemacht wurde. Benötigt werden schriftliche Addition und Division. Damit dies in absehbarar Zeit zu Erfolgen führt, soll die Genauigkeit nur drei Nachkommastellen betragen.
- Man erzeuge die Folge der Potenzen der Zahl 1,01 bis das Ergebnis 10 (die Basis) erreicht ist. D. h. wir beginnen mit der ersten Potenz (1,01), dann addieren wir die um zwei Stellen versetzte Zahl hinzu und erhalten die zweite Potenz: 1,01 + 0,0101 = 1,0201. So fahren wir fort, wobei wir nach der vierten Nachkommastelle runden: 3. Potenz ist 1,0303; 4. Potenz ist 1,0406;. .. Beim Runden müssen die mathematischen Rundungsregeln beachtet werden. Beispiel: 11. Potenz ist 1,1155; dann ist die 12. Potenz 1,1155 + 0,0112 = 1,1267.
Die 231. Potenz ist 9,959; die 232. Potenz ist 10,059. - Durch lineare Interpolation (für die 9. Klasse ggf. durch Streckenvergleich veranschaulichen) ergibt sich, dass 231,4 Schritte nötig wären, um genau 10,00 als Ergebnis zu erhalten.
- Um beispielsweise den Logarithmus der Zahl 2 zu ermitteln, ist die 2,00 unter den Ergebnissen aufzusuchen. Sie liegt zwischen der 69. Potenz (1,9867) und der 70. Potenz von 1,01 (2,0066). Linear interpoliert ergibt sich 69,7. Der gesuchte Logarithmus ergibt sich durch (schriftliche) Division: 69,7: 231,4 = 0,3012.
Da der genaue Wert 0,30103 ist, ist die gewünschte Genauigkeit erreicht. Historisch wurde mit 1,000001 gearbeitet.
Siehe auch
Weblinks
- Informationen über John Napier (University of St Andrews, Schottland) (engl.)
- vierstellige Logarithmentafel online
Wikimedia Foundation.

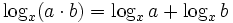
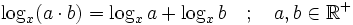
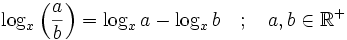

![\log_x \sqrt[b]{a} = \frac{1}{b} \cdot \log_x a \qquad \qquad; \quad a \in \mathbb{R}^+ \; \ b \in \mathbb{R} \setminus \{ 0\}](/pictures/dewiki/99/cd40b63258be5c30544ed24c56c97228.png)