Division (Mathematik)

20:4 = 5

Die Division ist eine der vier Grundrechenarten der Arithmetik. Sie ist die Umkehroperation der Multiplikation. Die Division wird umgangssprachlich auch als Teilen bezeichnet. Die schriftliche Division ist die Methode des Teilens mit Bleistift und Papier, die im Schulunterricht gelehrt wird.

Definition

In den Körpern der rationalen, reellen und komplexen Zahlen gilt:

Für jede Zahl a und für jede von null verschiedene Zahl b gibt es genau eine Zahl x, die die folgende Gleichung erfüllt:

$b \cdot x = a$   (wird „b mal x gleich a“ gelesen).

Die Umkehrung der Multiplikation zur Bestimmung von x heißt Division. x lässt sich bestimmen, indem man a durch b dividiert („teilt“):

$x = a : b\,$   (wird „x gleich a geteilt durch b“ gelesen).

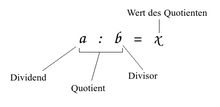
Die auftretenden Terme heißen wie folgt:

Die Zahl a, die geteilt wird, heißt „Dividend“ (Lateinisch wörtlich das zu teilende), umgangssprachlich „Zähler“.

Die Zahl b, durch die geteilt wird, heißt „Divisor“ (der Teiler), umgangssprachlich „Nenner“.

Der Term a:b heißt „Quotient“.

Das Ergebnis der Division heißt „Wert des Quotienten“.

Für die Division gilt weder das Kommutativgesetz noch das Assoziativgesetz.

Für x = a:b gilt außerdem $x = \tfrac{1}{b} \cdot a$.

Die Umkehrung der Multiplikation zur Bestimmung von x lässt sich also auch mit der Multiplikation der Umkehrung (Gegenteil) des 1 Faktors bestimmen.

Siehe auch: Kehrwert

Division durch null

Der Divisor muss ungleich null sein, da ansonsten der Quotient a:b als Lösung der Gleichung $b \cdot x = a$ für $b = 0\$ nicht eindeutig definiert ist:

Gäbe es zu einer gegebenen Zahl $a \ne 0$ eine Zahl $x = \tfrac{a}{0}$, so wäre diese Zahl Lösung der Gleichung $a = x \cdot 0 = 0$, womit sich ein Widerspruch zur Voraussetzung $a \ne 0$ ergeben würde, d. h. es gibt keine Lösung für x.

Wäre die Division von null durch null definiert, gäbe es also eine Zahl $x = \tfrac{0}{0}$, so wäre diese Zahl (eindeutige) Lösung der Gleichung $x \cdot 0 = 0$, also zu einer Gleichung, die für jedes $x\in\R$ richtig ist. Damit ist aber der Bruch $\tfrac{0}{0}$ nicht eindeutig definiert und ist daher unbestimmt.

Da also der Quotient a:0 entweder gar keine (für $a \neq 0$) oder mehr als eine Lösung (für a = 0) hat, sagt man allgemein:

„Die Division durch null ist nicht definiert.“

Division durch null im Computer

In elektronischen Rechnersystemen erzeugt eine Division durch null meist einen Laufzeitfehler, liefert NaN als Ergebnis oder wird anderweitig mit einer besonderen Behandlung abgefangen, da ein Weiterrechnen mit einem undefinierten Zwischenergebnis nicht sinnvoll wäre.

Division mit Rest

Im Bereich der ganzen Zahlen gilt: Eine Division ist nur dann gänzlich durchführbar, wenn der Dividend ein ganzzahliges Vielfaches des Divisors ist. Im Allgemeinen ist die Division hingegen nicht vollständig durchführbar, das heißt es bleibt ein Rest übrig. Siehe Hauptartikel: Division mit Rest.

Schreibweisen

Es gibt mehrere Schreibweisen für die Division (siehe hierzu Geteiltzeichen):

a:b   oder   $a \div b$   oder   a / b   oder   $\frac{a}{b}$.

Der Doppelpunkt als Zeichen für die Division ist erst seit Leibniz (1646–1716) allgemein üblich, wenngleich er auch in älteren Schriften bekannt ist. William Oughtred führte die Notation in seinem Werk Clavis Mathematicae von 1631 ein.

Die letzte erwähnte Schreibweise heißt auch Bruchdarstellung oder kurz (echter) Bruch. Die Bruchschreibweise ist nur bei kommutativer Multiplikation eindeutig; das spielt in allgemeineren mathematischen Strukturen eine Rolle, wie sie unten unter „Verallgemeinerung“ erwähnt werden.

„Unechter Bruch“ und „gemischte Zahl“

Als „unechten Bruch“ bezeichnet man einen Bruch, bei dem der Zähler einen größeren Betrag hat als der Nenner. Den Wert eines solchen Bruches gibt man normalerweise als „gemischte Zahl“ an, bestehend aus dem ganzzahligen Ergebnis der Division mit Rest und einem „echten Bruch“ aus Divisionsrest und Nenner, zum Beispiel:

$\frac{3}{2}=\frac{2}{2}+\frac{1}{2}=1+\frac{1}{2}=1\frac{1}{2}=1{,}5.$

Achtung, eine gemischte Zahl ist nicht mit einer Multiplikation zu verwechseln, bei der man gerne das Rechenzeichen auslässt:

$1\frac{1}{2}\neq1\cdot\frac{1}{2}.$

Üblicherweise schreibt man daher bei der Multiplikation einer Variable mit einem Bruch diesen nach vorne:

$a\cdot\frac{1}{2}=\frac{1}{2}\cdot a=\frac{1}{2}a.$

Verallgemeinerung

In der abstrakten Algebra definiert man algebraische Strukturen, die Körper genannt werden. Körper zeichnen sich dadurch aus, dass in ihnen die Division (außer durch 0) stets möglich ist. Die Division erfolgt hier durch Multiplikation mit dem inversen Element des Divisors.

In allgemeineren Strukturen (mit nichtkommutativer Multiplikation) muss man zwischen Linksdivision und Rechtsdivision unterscheiden. Auch hat die (Nicht-)Gültigkeit des Assoziativgesetzes Einfluss auf die Eigenschaften von Quotienten.

Siehe auch

• Rationale Funktion – Division von Funktionen
• Gruppentheorie
• Ring
• Schiefkörper
• Divisionsalgebra
• Teilbarkeit
• Kehrwert
• Polynomdivision
• Schriftliche Division
• Vedische Mathematik - Vereinfachte Methode zum Dividieren

Literatur

• S. A. Stepanov: Division. In: Michiel Hazewinkel (Hrsg.): Encyclopaedia of Mathematics. Springer-Verlag, Berlin 2002, ISBN 1-4020-0609-8.

Weblinks

 Commons: Division (mathematics) – Sammlung von Bildern, Videos und Audiodateien

 Wikibooks: Mathematik: Schulmathematik: Division – Lern- und Lehrmaterialien

 Wiktionary: Division – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen