- Lucas-Zahlen
-
Unter der Lucas-Folge versteht man zwei unterschiedliche Dinge:
- Einerseits die Folge
-
- 2, 1, 3, 4, 7, 11, 18, 29, ...
- bei der jedes Folgenglied (ab dem dritten) die Summe der beiden vorhergehenden ist.
- Andererseits die beiden allgemeinen Lucas-Folgen Un(P,Q) und Vn(P,Q), die abhängig von den Parametern P und Q definiert sind als diejenigen Folgen, die
-
 bzw.
bzw. 
- erfüllen und der Rekursionsformel
- Un = PUn − 1 − QUn − 2 für n > 1
- (entsprechend für Vn) genügen. Im Spezialfall P = 1 und Q = − 1 ist Un die Folge der Fibonacci-Zahlen, Vn die oben definierte spezielle Lucas-Folge.
Die Lucas-Folgen sind nach dem französischen Mathematiker Édouard Lucas benannt, der sich als erster mit ihnen beschäftigt hat.
Inhaltsverzeichnis
Explizite Formeln
Vorbereitung
Zur Bestimmung der Folgenglieder der allgemeinen Lucas-Folge muss vorbereitend die zugeordnete quadratische Gleichung gelöst werden.
Für die expliziten Formeln werden die beiden Lösungen a und b der quadratischen Gleichung
 benötigt. Es sind dies
benötigt. Es sind diesund
Ist P2 − 4Q < 0, so ist eine der beiden komplexen Wurzeln zu wählen. Welche der beiden Zahlen a und welche b genannt wird, ist hierbei nicht von Belang.
Die Parameter P und Q und die Werte a und b sind von einander abhängig, es gilt umgekehrt
Die Formeln für a und b lassen sich in Bezug auf die Potenzen verallgemeinern. Und zwar gilt:
Die allgemeinen Lucas-Folgen
Falls
 gilt, oder äquivalent dazu: falls die Zahlen a und b verschieden sind, so berechnet sich das Glied der allgemeinen Lucas-Folge
gilt, oder äquivalent dazu: falls die Zahlen a und b verschieden sind, so berechnet sich das Glied der allgemeinen Lucas-Folge  nach folgender Formel:
nach folgender Formel:für alle
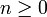 . Im Spezialfall P2 − 4Q = 0 gilt stattdessen
. Im Spezialfall P2 − 4Q = 0 gilt stattdessenDas Glied der allgemeinen Lucas-Folge
 berechnet sich nach folgender Formel:
berechnet sich nach folgender Formel:für alle
Beziehungen zwischen den Folgegliedern




 ; für alle
; für alle 
Spezialfälle
P Q a b U(P,Q) V(P,Q) 1 -1 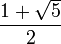

Fibonacci-Folge Lucas-Folge 2 -1 

Pell-Folge Companion Pell-Folge 1 -2 

Jacobsthal-Folge A+1 A A 1  mit
mit 
An+1 Folge 3 -10 5 -2 Folge A015528 in OEIS 4 -5 5 -1 Folge A015531 in OEIS 5 -6 6 -1 Folge A015540 in OEIS 8 -9 9 -1 Folge A015577 in OEIS Die allgemeine Lucas-Folgen Un(P,Q), Vn(P,Q) und die Primzahlen
Die Allgemeinen Lucas-Folgen
 und
und  haben für ganzzahlige Parameter P und Q eine spezielle Eigenschaft hinsichtlich der Teilbarkeit durch Primzahlen. Diese Eigenschaft wurde bei bestimmten Verfahren zur Bestimmung der Primalität einer Zahl angewandt. Leider waren diese Verfahren für bestimmte Arten von Pseudoprimzahlen anfällig.
haben für ganzzahlige Parameter P und Q eine spezielle Eigenschaft hinsichtlich der Teilbarkeit durch Primzahlen. Diese Eigenschaft wurde bei bestimmten Verfahren zur Bestimmung der Primalität einer Zahl angewandt. Leider waren diese Verfahren für bestimmte Arten von Pseudoprimzahlen anfällig.U(P,Q)
Für alle Lucas-Folgen
 gilt:
gilt:- Ist
 eine Primzahl, so ist
eine Primzahl, so ist  durch
durch  teilbar.
teilbar.
Dabei ist
 das Legendre-Symbol.
das Legendre-Symbol.Es existieren auch zusammengesetzte Zahlen, die diese Bedingung erfüllen. Diese Zahlen nennt man Lucas-Pseudoprimzahlen.
V(P,Q)
Für alle Lucas-Folgen
 gilt: wenn
gilt: wenn 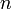 eine Primzahl ist, dann ist
eine Primzahl ist, dann ist  durch
durch 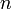 teilbar. Oder, anders ausgedrückt:
teilbar. Oder, anders ausgedrückt:für alle
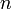 , die Primzahlen sind. Zusammengesetzte Zahlen die diese Bedingung erfüllen, mit der Einschränkung das
, die Primzahlen sind. Zusammengesetzte Zahlen die diese Bedingung erfüllen, mit der Einschränkung das  positiv und
positiv und  entweder 1 oder -1 ist, nennt man Fibonacci-Pseudoprimzahlen.
entweder 1 oder -1 ist, nennt man Fibonacci-Pseudoprimzahlen.Der kleine Fermatsche Satz
Besonders interessant ist dies für die Folge
 . Für diese Folge gilt nämlich:
. Für diese Folge gilt nämlich:- Wenn n eine Primzahl ist, dann gilt: n teilt
 .
.
Dies ist eine spezielle Form des kleinen Fermatschen Satz.
Analog zu
 gilt also
gilt also 
Anwendungen der allgemeinen Lucas-Folgen
Die allgemeinen Lucas-Folgen spielen in der Zahlentheorie und der Kryptographie eine Rolle.
Siehe auch: Lucas-Lehmer-Test, Lucassche Pseudoprimzahl, Fibonacci-Folge, Jacobsthal-Folge, Pell-Folge
Die spezielle Lucas-Folge
Die allgemein als Lucas-Folge bekannte Folge
 der Lucas-Zahlen 2 1 3 4 7 11 18 29 ... lässt sich auf unterschiedlichste Art und Weise erzeugen:
der Lucas-Zahlen 2 1 3 4 7 11 18 29 ... lässt sich auf unterschiedlichste Art und Weise erzeugen:- Über die Formel von Binet (nach Jacques Philippe Marie Binet):
 die sich aus der allgemeinen Lucas-Folge Ln = Vn( − 1,1) = an + bn mit a =
die sich aus der allgemeinen Lucas-Folge Ln = Vn( − 1,1) = an + bn mit a = 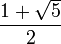 und b =
und b =  ableiten lässt
ableiten lässt
- Über die rekursive Formel, die der rekursiven Formel für die Fibonacci-Folge gleicht:
 mit den Anfangswerten
mit den Anfangswerten  und
und 
- Über eine Potenz des goldenen Schnitt:

- Eine andere rekursive Formel:
![L_{n+1} = \left[\frac{L_n(1+\sqrt{5})+1}{2}\right]](/pictures/dewiki/50/293d3f1eafb5f083b5f56cc8d3184bbd.png)
- Als Summe zweier Glieder der Fibonacci-Folge:

Siehe auch
Literatur
- Paulo Ribenboim: The new Book of Primenumber Records, ISBN 0-387-94457-5.
- Paulo Ribenboim: My Numbers, my Friends, ISBN 0-387-98911-0.
Weblinks
Wikimedia Foundation.



 (
(


