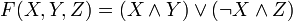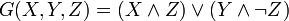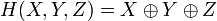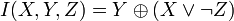MD-5

MD5 (Message-Digest Algorithm 5) ist eine weit verbreitete kryptographische Hashfunktion, die einen 128-Bit-Hashwert erzeugt. MD5 wurde 1991 von Ronald L. Rivest entwickelt. Die errechneten MD5-Summen (kurz md5sum) werden zum Beispiel zur Integritätsprüfung von Dateien eingesetzt.

Geschichte

MD5 ist ein Vertreter aus einer Reihe von (kryptologischen) Hashfunktionen, die von Ronald L. Rivest am Massachusetts Institute of Technology entwickelt wurden. Als Analysen ergaben, dass der Vorgänger MD4 wahrscheinlich unsicher ist, wurde MD5 1991 als sichererer Ersatz entwickelt. Tatsächlich wurden später von Hans Dobbertin Schwächen in MD4 gefunden.

1996 meldete Dobbertin eine Kollision in der Kompressionsfunktion von MD5. Dies war zwar kein Angriff auf die vollständige MD5-Funktion, dennoch empfahlen Kryptographen bereits damals, wenn möglich, auf sicherere Algorithmen wie SHA-256 oder RIPEMD-160 umzusteigen. Im August 2004 fanden chinesische Forscher Kollisionen für die vollständige MD5-Funktion. Wie sich diese Entdeckung auf die Verwendung von MD5 auswirkt, bleibt abzuwarten.

Diese Attacken wirken sich allerdings nur auf Kollisionsangriffe aus, Preimage-Angriffe können auch mit diesen Methoden nicht in sinnvoller Zeit durchgeführt werden. So kann ein bestehendes, mit MD5 erzeugtes Zertifikat nach wie vor nicht gefälscht werden.

Im Dezember 2008 führte jedoch eine Gruppe von Wissenschaftlern auf dem 25. Chaos Communication Congress vor, dass sie sich mit Hilfe eines Kollisionsangriffs ein vertrauenswürdiges CA-Zertifikat ausstellen lassen konnten^[1]. Zur Kollisionsberechnung benutzten sie einen Cluster von 200 Sony Playstation 3 und noch nicht veröffentlichte kryptographische Ergebnisse.

MD5-Hashes

Die 128 Bit langen MD5-Hashes (englisch auch „message-digests“) werden normalerweise als 32-stellige Hexadezimalzahl notiert. Folgendes Beispiel zeigt eine 59 Byte lange ASCII-Eingabe und den zugehörigen MD5-Hash:

md5("Franz jagt im komplett verwahrlosten Taxi quer durch Bayern") =
a3cca2b2aa1e3b5b3b5aad99a8529074

Eine kleine Änderung des Textes erzeugt mit sehr großer Wahrscheinlichkeit einen komplett anderen Hash. Mit Frank statt Franz (nur ein Buchstabe verändert) ergibt sich:

md5("Frank jagt im komplett verwahrlosten Taxi quer durch Bayern") =
7e716d0e702df0505fc72e2b89467910

Der Hash einer Zeichenfolge der Länge Null ist:

md5("") = d41d8cd98f00b204e9800998ecf8427e

Verwendung und Verfügbarkeit

MD5-Summen werden unter anderem von PGP verwendet und zur Integritätsprüfung von Dateien benutzt. Dabei wird die momentane MD5-Summe der Datei mit einer bekannten früheren Summe verglichen. So kann festgestellt werden, ob die Datei verändert oder beschädigt wurde. Unter den meisten Linux-Distributionen wird das Programm md5sum standardmäßig installiert, auf BSD-abgeleiteten Betriebssystemen wie Mac OS X gibt es das Kommando md5. Während man sich auf vielen anderen Unix-Derivaten noch mit dem meist installierten Programm OpenSSL behelfen kann, besitzen Microsoft-Windows-Betriebssysteme ab Werk kein Programm zur Berechnung von MD5-Hashes, jedoch ist auch für Windows eine Fülle von frei downloadbaren Versionen verfügbar; der De-facto-Standard ist md5sum.exe aus den GnuWin32-CoreUtils^[2]. Für Windows-Entwickler bietet die .NET-Plattform, die zunehmend Verbreitung findet, vorgebaute MD5-Algorithmen im Cryptographic-Namensraum. Da ihre spezielle Funktionsweise nicht offengelegt wurde, ist der Algorithmus jedoch als nicht vertrauenswürdig zu betrachten.

Überprüfung der MD5-Summe

Nach erfolgreichem Download einer Datei oder eines Ordners mit Dateien wird in der Regel in einer weiteren Datei die MD5-Summe mitgeteilt. Über ein Prüfsummen-Programm kann dann erneut die Prüfsumme aus der heruntergeladenen Datei berechnet werden, welche mit der mitgeteilten MD5-Summe verglichen wird. Sind beide MD5-Summen identisch, ist die Integrität der heruntergeladenen Datei bestätigt. Demnach traten beim Download der Datei keine Fehler auf.

Algorithmus

MD5-Algorithmus

MD5 erzeugt aus einer Nachricht variabler Länge eine Ausgabe fester Länge (128 Bit). Die Ausgangsnachricht wird zunächst so aufgefüllt, dass ihre Länge 64 Bits davon entfernt ist, durch 512 teilbar zu sein. Als erstes wird eine Eins angehängt, dann so viele Nullen wie nötig. In dem unwahrscheinlichen Fall, dass die Ausgangsnachricht schon die gewünschte Länge besitzt, wird trotzdem eine Eins angehängt. Nun wird eine 64-Bit-Zahl, die die Länge der Ausgangsnachricht repräsentiert, angehängt. Die Nachrichtenlänge ist jetzt durch 512 teilbar.

Der Hauptalgorithmus von MD5 arbeitet mit einem 128-Bit-Puffer, der in vier 32-Bit-Wörter A, B, C und D unterteilt ist. Diese werden mit bestimmten Konstanten initialisiert. Auf diesen Puffer wird nun die Komprimierungsfunktion mit dem ersten 512-Bit-Block als Schlüsselparameter aufgerufen. Die Behandlung eines Nachrichtenblocks geschieht in vier einander ähnlichen Stufen, von Kryptografen „Runden“ genannt. Jede Runde besteht aus 16 Operationen, basierend auf einer nichtlinearen Funktion „F“, modularer Addition und Linksrotation. Es gibt vier mögliche „F“-Funktionen, in jeder Runde wird davon eine andere verwendet:

$F(X,Y,Z) = (X\wedge{Y}) \vee (\neg{X} \wedge{Z})$

$G(X,Y,Z) = (X\wedge{Z}) \vee (Y \wedge \neg{Z})$

$H(X,Y,Z) = X \oplus Y \oplus Z$

$I(X,Y,Z) = Y \oplus (X \vee \neg{Z})$

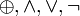$\oplus, \wedge, \vee, \neg$ stehen jeweils für XOR, AND, OR und NOT-Operationen.

Auf das Ergebnis wird dieselbe Funktion mit dem zweiten Nachrichtenblock als Parameter aufgerufen usw., bis zum letzten 512-Bit-Block. Als Ergebnis wird wiederum ein 128-Bit-Wert geliefert – die MD5-Summe.

Pseudocode

Es folgt der Pseudocode für den MD5-Algorithmus.

// Beachte: Alle Variablen sind vorzeichenlose 32-Bit-Werte und
// verhalten sich bei Berechnungen kongruent (≡) modulo 2^32

// Definiere r wie folgt:
var int[64] r, k
r[ 0..15] := {7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22}
r[16..31] := {5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20}
r[32..47] := {4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23}
r[48..63] := {6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21}

// Verwende den binären Vorkommateil vom 2^32-fachen Betrag des Sinus
// von Integerwerten als Konstanten:
für alle i von 0 bis 63
    k[i] := floor(abs(sin(i + 1)) × 2^32)

// Initialisiere die Variablen: (lt. RFC 1321)
var int h0 := 0x67452301
var int h1 := 0xEFCDAB89
var int h2 := 0x98BADCFE
var int h3 := 0x10325476

// Vorbereitung der Nachricht 'message':
var int message_laenge := bit_length(message)
erweitere message um bit "1"
erweitere message um bits "0" bis Länge von message in bits ≡ 448 (mod 512)
erweitere message um message_laenge als 64-Bit little-endian Integer

// Verarbeite die Nachricht in aufeinander folgenden 512-Bit-Blöcken:
für alle 512-Bit Block von message
    unterteile Block in 16 32-bit little-endian Worte w(i), 0 ≤ i ≤ 15

    // Initialisiere den Hash-Wert für diesen Block:
    var int a := h0
    var int b := h1
    var int c := h2
    var int d := h3

    // Hauptschleife:
    für alle i von 0 bis 63
        wenn 0 ≤ i ≤ 15 dann
            f := (b and c) or ((not b) and d)
            g := i
        sonst wenn 16 ≤ i ≤ 31 dann
            f := (b and d) or (c and (not d))
            g := (5×i + 1) mod 16
        sonst wenn 32 ≤ i ≤ 47 dann
            f := b xor c xor d
            g := (3×i + 5) mod 16
        sonst wenn 48 ≤ i ≤ 63 dann
            f := c xor (b or (not d))
            g := (7×i) mod 16
        wenn_ende
 
        temp := d
        d := c
        c := b
        b := ((a + f + k(i) + w(g)) leftrotate r(i)) + b 
        a := temp

    // Addiere den Hash-Wert des Blocks zur Summe der vorherigen Hashes:
    h0 := h0 + a
    h1 := h1 + b
    h2 := h2 + c
    h3 := h3 + d

var int digest := h0 append h1 append h2 append h3 //(Darstellung als little-endian)

Anstatt der Original-Formulierung aus dem RFC 1321 kann zur Effizienzsteigerung Folgendes verwendet werden:

(0 ≤ i ≤ 15): f := d xor (b and (c xor d))
(16 ≤ i ≤ 31): f := c xor (d and (b xor c))

Sicherheitsüberlegungen

MD5 ist weit verbreitet und wurde ursprünglich als kryptografisch sicher angesehen. Bereits 1994 entdeckten Bert den Boer und Antoon Bosselaers Pseudokollisionen in MD5. Grundlegende Arbeit, um echte Kollisionen zu finden, leistete auch Hans Dobbertin (damals am BSI), der bereits den erfolgreichen Angriff auf MD4 entwickelt hatte und die dabei verwendeten Techniken auf MD5 übertrug. Zwischenzeitlich war es ihm gelungen, eine in den Parametern modifizierte Version von MD5 zu brechen.

Die Brute-Force-Methode

Paul C. van Oorschot und Michael J. Wiener legten 1994 das Konzept eines Brute-Force-Angriffs auf MD5 vor, der mit Hilfe eines damals 10 Millionen US-Dollar teuren fiktiven Rechners durchgeführt werden sollte, der speziell auf diese Aufgabe ausgelegt war. Damit sollte es theoretisch möglich sein, innerhalb von 24 Tagen eine Kollision in MD5 zu finden. Im März 2004 startete das Projekt MD5CRK, das eine solche Kollision ohne Sonderinvestitionen finden wollte, indem man das Konzept des verteilten Rechnens ausnutzt. Obwohl eine Kollision ohne jede Kontrolle über die Ausgangsdaten zunächst wertlos erscheint, erhoffte man sich durch MD5CRK im Erfolgsfall auch psychologische Effekte auf Unternehmen, die sicherheitsrelevante Prozesse noch immer über MD5 absichern. Ein Test des Computermagazins c't unter Verwendung von GPGPU ermöglicht es einem etwa 1 Jahr alten Highend-Spiele-PC mit 2 nVidia GeForce 9800 GX2 in knapp 35 Minuten eine Kollision zu finden.

Neben dem obigen Angriff konnte Hans Dobbertin zeigen, dass die Kompressionsfunktion anfällig für Kollisionen ist. Diese Lücke konnte jedoch bisher nicht ausgenutzt werden.

Regenbogentabellen (Rainbow Tables)

Eine andere Angriffsmethode stellen Regenbogentabellen dar. In diesen Tabellen sind Zeichenketten mit den zugehörigen MD5-Hashwerten gespeichert. Der Angreifer durchsucht diese Tabellen nach dem vorgegebenen Hashwert und kann dann passende Zeichenketten auslesen. Dieser Angriff kann vor allem eingesetzt werden, um Passwörter zu ermitteln, die als MD5-Hashes gespeichert sind. Die dazu notwendigen Regenbogentabellen sind jedoch sehr groß und es bedarf eines hohen Rechenaufwands, um sie zu erstellen. Deshalb ist dieser Angriff im Allgemeinen nur bei kurzen Passwörtern möglich. Für diesen Fall existieren vorberechnete Regenbogentabellen, bei denen zumindest der Rechenaufwand zum Erstellen der Liste entfällt.

Die Analyse-Methode

Im August 2004 fand ein chinesisches Wissenschaftlerteam die erste Kollision in der vollständigen MD5-Funktion.^[3] Auf einem IBM-P690-Cluster benötigte ihr erster Angriff eine Stunde, davon ausgehend ließen sich weitere Kollisionen innerhalb von maximal fünf Minuten finden. Der Angriff der chinesischen Forscher basierte auf Analysen. Kurz nach der Veröffentlichung der Arbeit der Chinesen wurde MD5CRK eingestellt.

Kurzbeschreibung^[4]: Ein Eingabeblock (512 Bit) wird modifiziert, wobei versucht wird, eine bestimmte Differenz zum Original im Ausgang zu erzeugen. Durch eine aufwändige Analyse des Algorithmus kann die Anzahl der unbekannten Bits so weit verringert werden, dass dies rechnerisch gelingt. Im nächsten 512-Bit-Block wird mit den gleichen Methoden versucht, die Differenz wieder aufzuheben. Die Fälschung beschränkt sich also auf einen zusammenhängenden Datenblock von 1.024 Bit = 128 Byte, was den Einsatz stark einschränkt.

Kollisionen finden heißt, man kennt ein M (Text) und sucht ein M' (Kollision), so dass hash(M) = hash(M') (dies wäre eine Fälschung). Wenn man nur den Hashwert hat, ist es weiterhin schwierig, eine Kollision für den Hash zu finden (dies wäre eine zufällige Kollision). Die Kollisionsfreiheit von Algorithmen ist daher eine schwächere Forderung als die Fälschungssicherheit eines Hashwertes.

Deswegen besteht keine akute Gefahr für Passwörter, die als MD5-Hash gespeichert wurden, diese Kollisionen sind eher eine Gefahr für digitale Signaturen.

Literatur

• Hans Dobbertin: Cryptanalysis of MD5 compress. Announcement on Internet, Mai 1996 (englisch, online)
• Hans Dobbertin: The Status of MD5 After a Recent Attack. In: CryptoBytes 2(2), 1996 (englisch, online)
• Philip Hawkes, Michael Paddon, Gregory G. Rose: Musings on the Wang et al. MD5 Collision. Detaillierte Analyse der differentiellen Attacke auf den MD5 (englisch)
• Vlastimil Klima: Finding MD5 Collisions on a Notebook PC using multi-message modifications. Nochmals verbesserte Angriffstechnik (englisch)

Quellen

1. ↑ Sotirov, Alexander; Marc Stevens, Jacob Appelbaum, Arjen Lenstra, David Molnar, Dag Arne Osvik, Benne de Weger (30. Dezember 2008). MD5 considered harmful today. Abgerufen am 30. Dezember 2008.
2. ↑ http://gnuwin32.sourceforge.net/packages/coreutils.htm
3. ↑ Kollisionsanalyse
4. ↑ Erläuterung zum Kollisionsproblem bei Manipulation von md5-Hashwerten

Weblinks

• RFC 1321 – The MD5 Message-Digest Algorithm; R. Rivest, April 1992 (englisch)
• C++-Beispielimplementierung mit deutschsprachigen Kommentaren
• hashgenerator.de Online-Berechnung von MD5-Hashwerten zu einer eingegebenen Nachricht
• MD5 Collision Demo Zwei unterschiedliche Programme mit gleichem MD5-Hash und einer Bibliothek zur Generierung weiterer solcher Programme (englisch)
• Artikel "Hash mich, die zweite" von Jürgen Schmidt