Magisches Sechseck

Magisches Sechseck

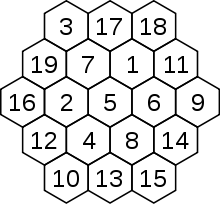
Ein magisches Sechseck ist eine sechseckige Anordnung von Zahlen, bei der die Summen aller Reihen in den drei Richtungen die gleiche Summe ergeben. Ein normales magisches Sechseck enthält die Zahlen von 1 bis 3n² − 3n + 1. Dies existiert nur für n=1 (trivial) und n=3 (nur eine Lösung wenn man Spiegelungen und Drehungen herausnimmt), welche die Summe 38 hat.

Bei n=3 gibt es für diese Zahlenbereiche auch Lösungen:

• 0−4 bis 14 mit der Summe 019: 36 Lösungen
• 0−9 bis 09 mit der Summe 000: 26 Lösungen (*)
• −14 bis 04 mit der Summe −19: 36 Lösungen (die gleichen Sechsecke wie bei „−4 bis 14“, nur alle Vorzeichen geändert)
• −19 bis −1 mit der Summe −38: 1 Lösung (das gleiche Sechseck wie im Bild oben, nur alle Zahlen negiert)

(*) 14 lassen sich durch komplette Vorzeichenänderung ineinander überführen; bei den restlichen 12 entspricht eine komplette Vorzeichenänderung einer Drehung um 180 Grad

Für n≥3 gibt es generell Lösungen. Für die Summe 0 muss man den Zahlenbereich − (3n² − 3n) / 2 bis (3n² − 3n) / 2 verwenden. Für von 0 abweichende Summen gilt dies, wenn i die Abweichung von 0 angibt:

kleinste Zahl:	i(2n − 1) − (3n2 − 3n) / 2
größte Zahl:	i(2n − 1) + (3n2 − 3n) / 2
Summe:	i(3n2 − 3n + 1)

(Bei i=2 und n=3 erhält man die oben stehende Lösung)

Eine Formel, die angibt, welche Werte i maximal bei einem gegebenen n haben kann, um noch eine oder mehrere Lösungen zu erhalten, ist bisher nicht bekannt.

Siehe auch

• Magisches Quadrat

Weblinks

 Commons: Magische Sechsecke – Sammlung von Bildern, Videos und Audiodateien

• http://www.math.uni-bielefeld.de/~sillke/PUZZLES/magic-hexagon