- Approximierbarkeit
-
Ein Approximationsalgorithmus ist in der Informatik ein Algorithmus, der ein Optimierungsproblem näherungsweise löst.
Viele Optimierungsprobleme lassen sich mit exakten Algorithmen nicht effizient lösen. Für solche Probleme kann es sinnvoll sein, wenigstens eine Lösung zu finden, die einer optimalen Lösung möglichst nahe kommt.
Güte von Approximationsalgorithmen
Es sei S(x) der zu einer Eingabe x gehörige Lösungsraum. Zu jeder möglichen Lösung
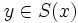 sei v(y) die Güte. Die Güte einer optimalen Lösung sei v * . Ein Approximationsalgorithmus sucht nun nach einer Lösung
sei v(y) die Güte. Die Güte einer optimalen Lösung sei v * . Ein Approximationsalgorithmus sucht nun nach einer Lösung 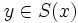 , so dass v(y) möglichst nah an v * liegt.
, so dass v(y) möglichst nah an v * liegt.Die Güte eines Approximationsverfahrens (sogenannte Approximationsgüte) wird durch die Performanz r des Algorithmus bestimmt. Sie ist definiert durch das Verhältnis von approximierter Lösung zur exakten Lösung, gemessen in einer angemessenen Norm. Die Performanz einer Lösung
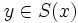 wird bestimmt durch:
wird bestimmt durch: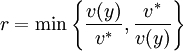
Diese Definition der Performanz kann sowohl auf Minimierungs- wie auch auf Maximierungsprobleme angewandt werden. Es gilt immer
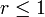 .
.Klassen von Approximationsalgorithmen
Optimierungsprobleme werden in der theoretischen Informatik in verschiedene Approximationsklassen unterschieden, je nachdem welcher Grad an Approximation möglich ist:
- APX
- Die Abkürzung APX steht für approximable und deutet an, dass das Optimierungsproblem, zumindest bis zu einem gewissen Grad, effektiv approximierbar ist.
- Ein Problem liegt in der Klasse APX, wenn eine Zahl
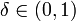 und ein polynomialer Algorithmus existiert, der bei jeder zulässigen Eingabe x eine Lösung mit einer Performanz
und ein polynomialer Algorithmus existiert, der bei jeder zulässigen Eingabe x eine Lösung mit einer Performanz 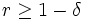 liefert.
liefert.
- PTAS/PAS
- PTAS oder PAS steht für polynomial time approximation scheme. Anders als bei der Klasse APX wird hier für jedes
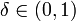 gefordert, dass ein polynomialer Algorithmus existiert, der bei jeder zulässigen Eingabe eine Lösung mit einer Performanz
gefordert, dass ein polynomialer Algorithmus existiert, der bei jeder zulässigen Eingabe eine Lösung mit einer Performanz 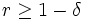 liefert. Der Algorithmus muss also nicht nur für eine bestimmte Performanz, sondern für jede Performanz effektiv sein, der Existenzquantor wird durch einen Allquantor ersetzt.
liefert. Der Algorithmus muss also nicht nur für eine bestimmte Performanz, sondern für jede Performanz effektiv sein, der Existenzquantor wird durch einen Allquantor ersetzt.
- FPTAS
- FPTAS steht für fully polynomial time approximation scheme. Hier wird gefordert, dass sich der Algorithmus nicht nur polynomial zur Eingabe, sondern auch zur Güte der Approximation verhält. Dass es also zu jeder Eingabe x und jedem
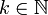 eine Lösung mit der Performanz
eine Lösung mit der Performanz 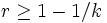 gibt, wobei der Algorithmus polynomial in x und k ist.
gibt, wobei der Algorithmus polynomial in x und k ist.
Es gilt:
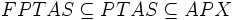
Unter der Annahme
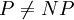 sind die obigen Inklusionsabbildungen echte Inklusionen. Das heißt es gibt zum Beispiel mindestens ein Optimierungsproblem, das in der Klasse PTAS liegt, aber nicht in der Klasse FPTAS.
sind die obigen Inklusionsabbildungen echte Inklusionen. Das heißt es gibt zum Beispiel mindestens ein Optimierungsproblem, das in der Klasse PTAS liegt, aber nicht in der Klasse FPTAS.Fasst man die Inklusionskette etwas weiter:
hieße das auch, dass es Optimierungsprobleme gibt, die nicht einmal in APX liegen. Dies lässt sich unter der Annahme das
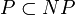 zum Beispiel für das Cliquenproblem zeigen.
zum Beispiel für das Cliquenproblem zeigen.Siehe auch
Wikimedia Foundation.

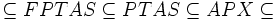 {Optimierungsprobleme in
{Optimierungsprobleme in