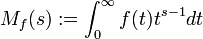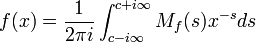Mellintransformation

In der Mathematik versteht man unter der Mellin-Transformation einer auf der positiven reellen Achse definierten Funktion f das Integral

$M_f(s) := \int_{0}^\infty f(t)t^{s-1}dt$

für komplexe Zahlen s, sofern dieses Integral konvergiert.

Sie ist benannt nach dem finnischen Mathematiker Hjalmar Mellin. In der Literatur findet man die Transformierte gelegentlich mit einem Normierungsfaktor 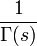$1 \over {\Gamma(s)}$, dabei ist Γ(s) die Gamma-Funktion. Die Mellin-Transformation ist eng verwandt mit der Fourier-Transformation. Substituiert man nämlich im obigen Integral t = e^x, setzt man F(x) = f(e^x) und bezeichnet man die Fourier-Transformierte der Funktion F mit $\widehat F$, so ist

$M_f(is) = \sqrt{2\pi}\widehat F(s)$.

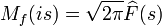Unter bestimmten Bedingungen ist die Rücktransformation möglich, es gilt dann

$f(x) = \frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty} M_f(s)x^{-s}ds$

mit einem c > 0.

Mittels der Mellin-Transformation lassen sich eine Dirichletreihe und eine Potenzreihe zueinander in Beziehung setzen. Es seien

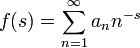$f(s) = \sum_{n=1}^\infty a_nn^{-s}$ und $F(z) = \sum_{n=1}^\infty a_nz^n$

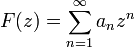
mit den gleichen a_n. Dann gilt

$f(s) = \frac{1}{\Gamma(s)} \int_0^\infty F(e^{-t})t^{s-1}dt$.

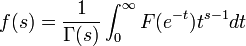Setzt man hier alle a_n = 1, so ist f die riemannsche Zetafunktion, und man erhält

$\zeta(s) = \frac{1}{\Gamma(s)} \int_0^\infty \frac{t^{s-1}}{e^t-1}dt$.

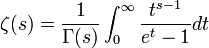Literatur

• M. Koecher, A. Krieg, Elliptische Funktionen und Modulformen, Springer-Verlag Berlin Heidelberg New York 1998, ISBN 3-540-63744-3
• R. Remmert, Funktionentheorie I, Springer-Verlag Berlin Heidelberg New York 1989, ISBN 3-540-51238-1
• E. C. Titchmarsh, Introduction to the Theory of Fourier Integrals, Chelsea Publishing Company, 3. Auflage 1986, ISBN 978-0828403245
• D. Zagier, Zetafunktionen und quadratische Körper, Springer-Verlag Berlin Heidelberg New York 1981, ISBN 3-540-10603-0