Missing-square-puzzle

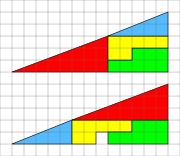
Das Fehlendes-Quadrat-Rätsel ist eine optische Täuschung aus der Geometrie.

Beschreibung

Animiertes Fehlendes-Quadrat-Rätsel

Fehlendes-Quadrat-Rätsel
Oben: Dreieck 1
Unten: Dreieck 2

Zwei scheinbar gleich große, rechtwinklige Dreiecke mit der Fläche 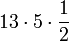$13\cdot5\cdot\frac{1}{2}$ werden verglichen. Die Maßeinheit ist grundsätzlich egal, hier werden jedoch zur besseren Veranschaulichung Zentimeter benutzt.

Jedes Dreieck besteht aus den gleichen Flächen:

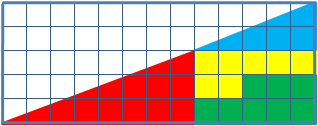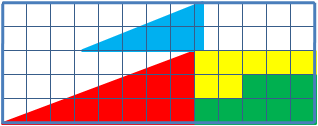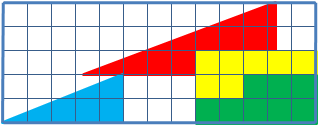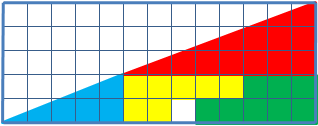
• ein rechtwinkliges Dreieck (hier: blau) mit einer Fläche von
  $5 \cdot 2 \cdot \frac{1}{2}\ \mathrm{cm^2}\ =\ 5\ \mathrm{cm^2}$
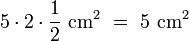
• ein weiteres Dreieck (hier: rot) mit einer Fläche von
  $8 \cdot 3 \cdot \frac{1}{2}\ \mathrm{cm^2}\ =\ 12\ \mathrm{cm^2}$
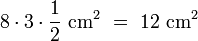
• zwei weiteren Formen (hier: gelb und grün), die zusammen ein Rechteck mit der Größe von
  $5\cdot 3\ \mathrm{cm^2}\ =\ 15\ \mathrm{cm^2}$
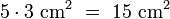
  hiervon entfallen
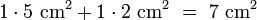  $1 \cdot 5\ \mathrm{cm^2}+1 \cdot 2\ \mathrm{cm^2}\ =\ 7\ \mathrm{cm^2}$ auf gelb und
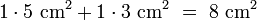  $1 \cdot 5\ \mathrm{cm^2}+1 \cdot 3\ \mathrm{cm^2}\ =\ 8\ \mathrm{cm^2}$ auf grün

Obwohl beide optisch gleichgroßen Dreiecke aus den augenscheinlich gleichen Teilflächen bestehen, ist beim Dreieck 2 ein Quadrat der Größe 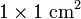$1 \times 1\ \mathrm{cm^2}$ übrig.

Erklärung

Darstellung der Flächenabweichung

Eine weitere optische Täuschung

Die einzelnen Flächen (rot, blau, grün und gelb) ergeben in der Addition eine Gesamtfläche von $5\ \mathrm{cm^2}+12\ \mathrm{cm^2}+7\ \mathrm{cm^2}+8\ \mathrm{cm^2}\ = \ 32\ \mathrm{cm^2}$

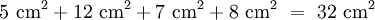
Ein korrektes Dreieck mit Katheten der Länge von 13 cm und 5 cm hat eine Fläche von $13\cdot5\cdot\frac{1}{2}\ \mathrm{cm^2}\ = \ 32,5\mathrm{cm^2}$.
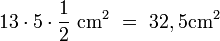Dadurch ist der mathematische Beweis erbracht, dass sich das gegebene Dreieck nicht aus den einzelnen Figuren erstellen lässt.

Ausgehend von den Flächen gegebener Teilstücke hat das zusammengesetzte, in oberen Abbildung dargestellte „Dreieck“ eine Fläche von 32 cm², in der unteren Abbildung jedoch eine Fläche von 33 cm² und somit 1 cm² mehr.

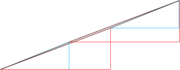
Dies resultiert aus den unterschiedlichen Winkeln des roten und blauen Dreiecks (sie sind nicht ähnlich im geometrischen Sinn). Daher haben beide zusammengesetzten „Dreiecke“ einen leichten Knick am Übergang vom roten zum blauen Teildreieck. Mathematisch lässt sich dies wie folgt beweisen:

• blaues Dreieck:
  $\arctan\left(\frac{2}{5}\right)=\arctan\left(0,4\right)=21,8\,^{\circ}$
• rotes Dreieck:
  $\arctan\left(\frac{3}{8}\right)=\arctan\left(0,375\right)=20,56\,^{\circ}$
• zum Vergleich der Winkel eines Dreiecks mit Katheten der Länge von 13 und 5:
  $\arctan\left(\frac{5}{13}\right)=\arctan\left(0,385\right)=21,04\,^{\circ}$

Die obere Kante ist also keine Gerade. Erkennen kann man dies jeweils am Übergang von rot zu blau, wo sich ein Knick befindet. Somit ist die zusammengesetzte Figur jeweils überhaupt kein echtes Dreieck, sondern das Dreieck 1 ein konkaves und Dreieck 2 ein konvexes Viereck, deren Flächeninhalte sich um 1 cm² unterscheiden.

Bei der Papierversion, bei der man die Flächen per Hand ausschneiden kann, wird der Knick durch eine dick gezeichnete Randlinie verdeckt. Des Weiteren ist das Ausschneiden und Zusammenfügen viel zu ungenau, dass man den Unterschied sehen könnte.

Weblinks

• Curry's Paradox: How Is It Possible? (englisch)
• Triangles and Paradoxes (englisch)