Mitchell-Netravali-Filter

Die Mitchell-Netravali-Filter oder BC-Splines sind eine vorrangig in der Computergrafik verwendete Gruppe von Rekonstruktionsfiltern, die zum Beispiel beim Antialiasing oder bei der Skalierung von Rastergrafiken verwendet werden können. In Bildbearbeitungsprogrammen werden sie auch als bikubische Filter bezeichnet, da sie zu den kubischen Splines zählen.

Definition

Graph des Mitchell-Netravali-Filters mit Parameterwahl (⅓, ⅓)

Die Mitchell-Netravali-Filter wurden im Rahmen einer Untersuchung zu Artefakten von Rekonstruktionsfiltern entworfen. Die Filter sind stückweise kubische Filter mit vier Pixel breiten Trägern. Nach Ausschluss ungeeigneter Filter aus dieser Familie, wie zum Beispiel unstetige Kurven, verbleiben zwei Parameter B und C, durch die die Mitchell-Netravali-Filter konfigurierbar sind. Die Filter sind wie folgt definiert:

$k(x) = \frac{1}{6} \begin{cases} \begin{align} (12-9B-6C)|x|^3 + (-18+12B+6C)|x|^2 \\ + (6-2B) \end{align} & \text{, wenn } |x|<1 \\ \begin{align} (-B-6C)|x|^3 + (6B+30C)|x|^2 \\ + (-12B-48C)|x| + (8B+24C) \end{align} & \text{, wenn } 1\le |x|<2 \\ 0 & \text{ansonsten} \end{cases}$

Es ist möglich, zweidimensionale Versionen der Mitchell-Netravali-Filter durch Separation zu konstruieren. In diesem Fall können die Filter durch eine Reihe von Interpolationen mit dem eindimensionalen Filter ersetzt werden. Aus den Farbwerten der vier benachbarten Pixel P₀, P₁, P₂, P₃ berechnet sich dann der Farbwert P(d) folgendermaßen:

$\begin{align} P(d) &\textstyle = \left((-\frac{1}{6}B-C)P_0 + (-\frac{3}{2}B-C+2)P_1 + (\frac{3}{2}B+C-2)P_2 + (\frac{1}{6}B+C)P_3\right) d^3 \\ &\textstyle + \left((\frac{1}{2}B+2C)P_0 + (2B+C-3)P_1 + (-\frac{5}{2}B-2C+3)P_2 -CP_3\right) d^2 \\ &\textstyle + \left((-\frac{1}{2}B-C)P_0 + (\frac{1}{2}B+C)P_2\right) d \\ &\textstyle + \frac{1}{6}BP_0 + (-\frac{1}{3}B+1)P_1 + \frac{1}{6}BP_2 \\ \end{align}$

P liegt hierbei zwischen P₁ und P₂; d ist der Abstand zwischen P₁ und P.

Spezialfälle

Subjektives Aussehen von mit Mitchell-Netravali-Filtern rekonstruierten Bildern. Die gestrichelte Linie markiert eine von den Entwicklern als guter Kompromiss empfohlene Parameterfamilie.

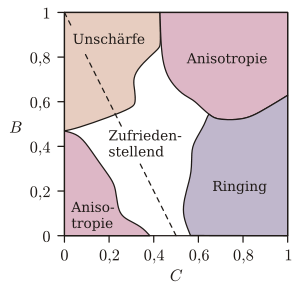
Je nach Wahl der Parameter B und C kann es zu verschiedenen Artefakten kommen (siehe Bild rechts). Die Entwickler schlugen die Parameter aus der Familie B + 2C = 1 und besonders $\textstyle B=C=\frac{1}{3}$ als guten Kompromiss vor.

Die Wahl bestimmter Parameter führt zu bekannten kubischen Splines:

• B=1, C=0 ist der kubische B-Spline (als bikubischer Filter z.B. in Paint.NET verwendet);
• B=0 ist die Familie der Cardinal Splines;
• B=0, C=0,5 ist der Catmull-Rom Spline (als bikubischer Filter z.B. in GIMP verwendet).

Vergrößerung mit bikubischem Filter in GIMP (B=0, C=0,5)

Vergrößerung mit bikubischem Filter in Paint.NET (B=1, C=0)

Weblinks

• The eighties: an image processing view – Thomas Teußl: Sampling and Reconstruction in Volume Visualization (Diplomarbeit)

Literatur

• Don Mitchell, Arun Netravali: Reconstruction Filters in Computer Graphics. ACM SIGGRAPH Computer Graphics 22, 4 (Aug. 1988): 221–228, ISSN 0097-8930
• Matt Pharr, Greg Humphreys: Physically Based Rendering. From Theory to Implementation, S. 279–367. Morgan Kaufmann, London 2004, ISBN 01-2553-180-X (PDF, 7 MB)