Monge-Ampere-Gleichung

Eine monge-ampèresche Gleichung, oder monge-ampèresche Differentialgleichung, ist eine spezielle nichtlineare partielle Differentialgleichung zweiter Ordnung in n Variablen.

Sie wurde von Gaspard Monge Anfang des 19. Jahrhunderts eingeführt, um ein Massentransportproblem ("problème du remblai-déblai", etwa: "Problem von Erdaufschüttung und -aushub") für militärische Zwecke zu lösen. Trotz ihrer recht einfachen Form ist sie im Allgemeinen schwierig zu lösen.

Mathematische Formulierung

Allgemein hat eine monge-ampèresche Gleichung über einem offenen Gebiet 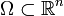$\Omega \subset \mathbb{R}^n$ die Form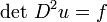

  $\det\, D^2 u = f$

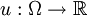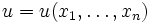wobei $u: \Omega \to \mathbb{R}$, mit $u = u(x_1, \ldots, x_n)$ die unbekannte Funktion ist, 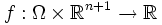$f: \Omega \times \mathbb{R}^{n+1} \to \mathbb{R}$ eine gegebene Funktion 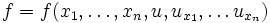$f = f(x_1, \ldots, x_n, u, u_{x_1}, \ldots u_{x_n})$, und

$D^2 u = \begin{pmatrix} u_{x_1x_1} & \cdots & u_{x_1 x_{n}} \\ \vdots & \ddots & \vdots \\ u_{x_n x_1} & \cdots & u_{x_n x_n} \end{pmatrix} \qquad \mbox{mit } u_{x_i x_j} = \frac{\partial^2 u}{\partial x_i \partial x_j}.$

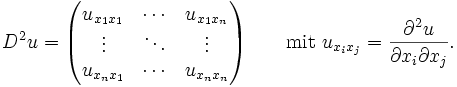
die Hesse-Matrix von u. Speziell für den zweidimensionalen Fall n=2 ergibt sich die einfache Gestalt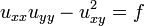

  $u_{xx} u_{yy} - u_{xy}^2 = f$

mit 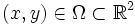$(x,y) \in \Omega \subset \mathbb{R}^2$ und den Funktionen u(x,y) und f(x,y,u,u_x,u_y). Oft wird für den Fall n=2 aber auch die folgende Darstellung als allgemeine monge-ampèresche Gleichung bezeichnet: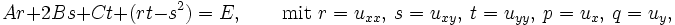

  $Ar + 2Bs + Ct + (rt - s^2) = E, \qquad \mbox{mit } r=u_{xx},\ s=u_{xy},\ t=u_{yy},\ p=u_x,\ q=u_y,$

wobei A, B, C und E Funktionen von (x, y, u, p, q) sind. Man erkennt gleich, dass sich mit A=B=C=0 und E=f die obige einfachere Gestalt ergibt.

Konkretes Beispiel

Sei n=2 und f(x,y) = 4(1 − y²)(1 − x²) − 16x²y². Dann ist u(x,y) = (1 − x²)(1 − y²) eine Lösung der monge-ampèreschen Differentialgleichung, denn u_xx = − 2(1 − y²), u_yy = − 2(1 − x²), u_xy = u_yx = − 4xy, und daher $\det\, D^2 u = \det \begin{pmatrix} -2(1-y^2) & -4xy \\ -4xy & -2(1-x^2) \end{pmatrix} = f(x,y).$

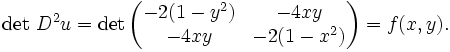
Klassifizierung als partielle Differentialgleichung

Eine monge-ampèresche Gleichung ist eine voll nichtlineare partielle Differentialgleichung zweiter Ordnung in n Variablen. Erläuterungen:

• "partielle Differentialgleichung", denn es wird eine von mehreren Variablen abhängende Funktion u gesucht, deren partielle Ableitungen der gegebenen Gleichung gehorchen müssen.

• "voll nichtlinear", da alle Terme mit zweiten (also den höchsten) Ableitungen von u quadratisch auftauchen.

Eine wichtige Klasse sind die elliptischen monge-ampèrescher Gleichungen, die für n=2 die Bedingungen AC − B² + E > 0 und t + A > 0 erfüllen, bzw. in der einfacheren Form einfach f > 0.

Anwendungen

Die meisten Anwendungen der monge-ampèreschen Gleichung sind innermathematischer Art. Beim Minkowski-Problem beispielsweise wird eine strikt konvexe Hyperfläche mit vorgegebener Gaußkrümmung gesucht, was auf eine monge-ampèresche Gleichung führt. Das Problem wurde 1953 von Nirenberg gelöst.

Eine unerwartete Anwendung im Bereich der String-Theorie ergab sich durch ein 1978 veröffentlichtes Resultat von Yau, der eine Vermutung von Calabi über die Krümmung bestimmter Kähler-Mannigfaltigkeiten mit Hilfe der Lösung einer komplexen monge-ampèreschen Gleichung bewies (Satz von Yau). Man spricht heute entsprechend von Calabi-Yau-Mannigfaltigkeiten.

Bedeutende Beiträge zu monge-ampèreschen Gleichungen im Verlaufe des 20. Jahrhunderts kamen von Hermann Weyl, Franz Rellich, Erhard Heinz, Louis Nirenberg, Shing-Tung Yau, Luis Caffarelli.

Weblinks

• Plots von Lösungen Monge-Ampèrescher Gleichungen
• Eintrag in MathWorld (engl.)