Mordellsche Vermutung

Die Vermutung von Mordell entstammt der Zahlentheorie, wurde im Jahr 1922 von Louis Mordell aufgestellt und 1983 von Gerd Faltings in seinem Artikel Endlichkeitssätze für abelsche Varietäten über Zahlkörpern^[1] (Faltings' Satz) bewiesen.

Problemstellung und Historie

Wenn K ein Zahlkörper und C eine nichtsinguläre Kurve definiert über K sind, dann besteht die Frage, wie viele Punkte der Kurve C(K) selbst Koordinaten in K haben.

• Falls das Geschlecht g von C gleich 0 ist, ist C isomorph zum eindimensionalen projektiven Raum über dem algebraischen Abschluss von K, also 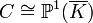$C \cong \mathbb{P}^1(\overline{K})$. Daher kann C(K) leer oder eine unendliche Menge 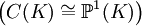$\left( C(K) \cong \mathbb{P}^1(K) \right)$ sein.
• Im Fall g = 1 ist bekannt: wenn C(K) mindestens einen Punkt mit Koordinaten in K hat, dann sind C eine elliptische Kurve und C(K) eine endlich erzeugte abelsche Gruppe. Letzteres ist als Satz von Mordell-Weil geläufig und impliziert, dass C(K) endlich oder unendlich sein kann.

Von besonderem Interesse ist dabei der Fall des Körpers der rationalen Zahlen, für den die Vermutung ursprünglich von Louis Mordell formuliert war. Nach dem Satz gibt es für Kurven vom Geschlecht g größer 1 nur endlich viele rationale Punkte auf der Kurve. Kurven über den rationalen Zahlen zeigen also wesentlich verschiedenes Verhalten für g=0,g=1 und g größer 1 - eine topologische Größe bestimmt das zahlentheoretische Verhalten. Für ganze Zahlen hatte das schon Carl Ludwig Siegel in den 1920er Jahren bewiesen.

Formulierung der Vermutung und Hinweise zum Beweis durch Faltings

Seien K ein Zahlkörper und C eine nichtsinguläre Kurve definiert über K vom Geschlecht g > 1. Dann ist C(K) endlich.

In seiner Arbeit bewies er auch die Tate-Vermutung von John T. Tate und die Vermutung von Igor Shafarevich, indem er den Übersetzungsmechanismus von Funktionenkörpern auf Zahlkörper von Suren Arakelov ausbaute.

Sonstiges

Auf anderem Weg hat nach Faltings Paul Vojta den Satz bewiesen.

Faltings trug seinen Beweis zuerst auf der mathematischen Arbeitstagung in Bonn am 17. und 19. Juli 1983 vor. 1986 erhielt er dafür die höchste Auszeichnung für Mathematiker, die Fields-Medaille. Manchmal wird die Vermutung von Mordell, die ja nun ein bewiesener Satz ist, nach Faltings Satz von Faltings genannt.

Der Satz liefert auch einen wichtigen Beitrag zum Beweis der fermatschen Vermutung, denn die fermatsche Gleichung xⁿ + yⁿ = 1 hat nach ihm für 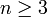$n \geq 3$ nur endlich viele rationale Lösungen.

Literatur

• Spencer Bloch: The proof of the Mordell conjecture. Mathematical Intelligencer, Bd. 6, 1984, S.41.
• Gerd Faltings: Die Vermutungen von Tate und Mordell. Jahresbericht Deutscher Mathematikerverein, 1984, S.1-13.

Weblinks

• Lucien Szpiro: La conjecture de Mordell. Séminaire Bourbaki Nr.619, 1983/84

Quellen

1. ↑ Invent. Math. 73 (3): 349-366, bzw. errata