Morley-Dreieck

Morley-Dreieck

Morley-Dreieck ist ein Begriff aus der Dreiecksgeometrie. Es ist folgendermaßen definiert:

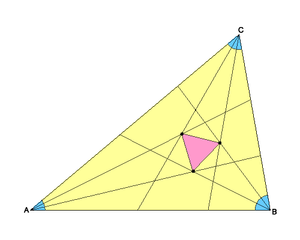
Die Innenwinkel eines beliebigen Dreiecks werden jeweils in drei gleich große Winkel unterteilt (was bekanntlich im Allgemeinen mit Zirkel und Lineal nicht möglich ist). Zu jeder Dreiecksseite betrachtet man den Schnittpunkt derjenigen zwei Teilungslinien, die von den Endpunkten dieser Seite ausgehen und zu dieser Seite benachbart sind. Das Morley-Dreieck ist das Dreieck, dessen Ecken die drei erhaltenen Schnittpunkte sind.

Unabhängig von der Form des ursprünglichen Dreiecks ist das Morley-Dreieck stets gleichseitig (Satz von Morley).^[1]

Siehe auch

Ausgezeichnete Punkte im Dreieck

Literatur

• H. S. M. Coxeter und S. L. Greitzer: Zeitlose Geometrie. Klett, Stuttgart 1983.

Weblinks

• Satz von Morley - Visualisierung mit GeoGebra
• Florian Modler: Vergessene Sätze am Dreieck. Teil 8: Der Schmetterling und der Satz von Morley auf Matroids Matheplanet
• Eric W. Weisstein: Morley's Theorem. In: MathWorld. (englisch)
• Eric W. Weisstein: First Morley Triangle. In: MathWorld. (englisch)

Einzelnachweise

1. ↑ Max Koecher, Aloys Krieg: Ebene Geometrie, 3. Aufl., Springer-Verlag, Berlin 2007, ISBN 978-3-540-49327-3, S. 131