N-Gram-Analyse

Ein N-Gramm ist eine Folge aus N Zeichen, beispielsweise ein Wortfragment. N-Gramme finden Anwendung in der Kryptologie und Linguistik, speziell auch in der Computerlinguistik, Computerforensik und Quantitativen Linguistik. Einzelne Wörter, ganze Sätze oder komplette Texte werden hierbei zur Analyse oder statistischen Auswertung in N-Gramme zerlegt.

Arten von N-Grammen

Wichtige N-Gramme sind das Monogramm, das Bigramm (manchmal auch als Digramm bezeichnet) und das Trigramm. Das Monogramm besteht aus einem Zeichen, beispielsweise nur aus einem einzelnen Buchstaben, das Bigramm aus zwei und das Trigramm aus drei Zeichen. Allgemein kann man auch von Multigrammen sprechen, wenn es sich um eine Gruppe von „vielen“ Zeichen handelt.

Die Vorsilben der Bezeichnungen werden in der Regel unter Zuhilfenahme der griechischen Zahlwörter gebildet. Beispiele sind mono für „allein“ oder „einzig“, tri für „drei“, tetra für „vier“, penta für „fünf“, hexa für „sechs“, hepta für „sieben“, okto für „acht“ und so weiter. Bi und multi sind Vorsilben lateinischen Ursprungs und stehen für „zwei“ beziehungsweise „viele“.

Die folgende Tabelle gibt sortiert nach der Anzahl der Zeichen N zusammen mit einem Beispiel, bei denen als Zeichen Alphabet-Buchstaben genommen wurden, eine Übersicht über die Bezeichnung der N-Gramme:

N-Gramm-Name	N	Beispiel
Monogramm	1	A
Bigramm	2	AB
Trigramm	3	UNO
Tetragramm	4	HAUS
Pentagramm	5	HEUTE
Hexagramm	6	SCHIRM
Heptagramm	7	TELEFON
Oktogramm	8	COMPUTER
…	…	…
Multigramm	N	BEOBACHTUNGSLISTE

Formale Definition

Sei Σ ein endliches Alphabet und sei n eine positive ganze Zahl. Dann ist ein n-Gramm ein Wort w der Länge n über dem Alphabet Σ, d. h. $w=(w_1,\ldots,w_n)\in \Sigma^n$.

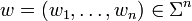Analyse

Die N-Gramm-Analyse wird verwendet, um die Frage zu beantworten, wie wahrscheinlich auf eine bestimmte Buchstaben- oder Wortreihenfolge ein bestimmter Buchstabe oder ein bestimmtes Wort folgen wird, beispielsweise die englischen Zeichen „for ex…“. Die bedingten Wahrscheinlichkeiten für die Buchstaben des Alphabets in der englischen Sprache sind in absteigender Rangreihenfolge: a = 0.4, b = 0.00001, c = 0, … mit einer Gesamtsumme von 1. Auf der Grundlage der n-Gramm-Häufigkeiten erscheint also eine Fortsetzung des Fragmentes mit „a“ -> „for exa(mple)“ deutlich wahrscheinlicher als die Alternativen.

Die verwendete Sprache ist für die Analyse nicht von Bedeutung, wohl aber ihre Statistik: Die N-Gramm-Analyse funktioniert in jeder Sprache und jedem Alphabet. Somit hat sich die Analyse in den Feldern der Sprachtechnologie bewährt: Zahlreiche Ansätze der maschinellen Übersetzung bauen auf den Daten gewonnen aus dieser Methode auf.

Besondere Bedeutung bekommt die Analyse, wenn große Datenmengen, z. B. E-Mails auf ein bestimmtes Themengebiet hin untersucht werden sollen. Durch die Ähnlichkeit mit einem Referenzdokument, z. B. einem technischen Bericht über Atombomben, Polonium, etc., lassen sich Cluster bilden. Je näher eine Mail am Referenzdokument liegt, umso wahrscheinlicher ist, dass sich der Inhalt um sein Thema dreht und – in unserem Beispiel evtl. Terrorismus-relevant sein könnte, selbst wenn die Schlüsselwörter nicht selbst auftauchen.

Kommerziell verfügbare Programme, die diese fehlertolerante und äußerst schnelle Methode ausnutzen, sind Rechtschreibprüfungen und Forensik-Werkzeuge (z. B. Computer Associates eTrust Network Forensics – Context).

Google-Korpus

Die Firma Google veröffentlichte im Jahr 2006 6 DVDs gefüllt mit englischsprachigen N-Grammen, die bei der Indexierung des Web entstanden. Diese sind jetzt für alle Welt zugänglich. Hier ein Beispiel aus dem Google-Korpus:

3-grams

ceramics collectables collectibles (55)

ceramics collectables fine (130)

ceramics collected by (52)

ceramics collectible pottery (50)

ceramics collectibles cooking (45)

4-grams

serve as the incoming (92)

serve as the incubator (99)

serve as the independent (794)

serve as the index (223)

serve as the indication (72)

serve as the indicator (120)

Beispiel

Eine zu durchsuchende Zeichenkette lautet: s={"Welcome to come"}.

n = 2 (sog. Bigramm)

Die Häufigkeit des Vorkommens der einzelnen Bigramme wird bestimmt.

Somit lautet der „Frequenzvektor“ f für die Zeichenkette s:

_W:1

We:1

el:1

lc:1

co:2

om:2

me:2

e_:1

_t:1

to:1

o_:1

_c:1

D.h. f = (1,1,1,1,2,2,2,1,1,1,1,1). Die Länge des Vektors ist dabei durch 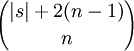${|s|+2(n-1)\choose n}$ nach oben beschränkt.

Dice-Koeffizient

Über N-Gramme lassen sich wie beschrieben Wort-Ähnlichkeiten berechnen. Ein Algorithmus dafür ist der Dice-Algorithmus. Der Dice-Koeffizient d zweier Terme a und b ist dabei definiert durch:

$d(a,b) = \frac{2|T(a) \cap T(b)|}{|T(a)|+|T(b)|}$

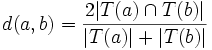
wobei T(x) eine N-Gram Zerlegung des Terms x ist. d liegt dabei immer zwischen 0 und 1.

Siehe auch: Distanzfunktion

Beispiel

• Term a = "wirk"
• Term b = "work"

Wenn wir Tri-Gramme benutzen, so sieht die Zerlegung folgendermaßen aus:

• T(a) = {§§w, §wi, wir, irk, rk§, k§§}
• T(b) = {§§w, §wo, wor, ork, rk§, k§§}

• T(a) 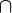$\cap$ T(b) = {§§w, k§§, rk§}

D.h. d(wirk, work) = 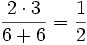$\frac{2\cdot3}{6+6} = \frac{1}{2}$. Der Dice-Koeffizient (man kann auch sagen die Ähnlichkeit) beträgt also 0.5 (50 %).

Anwendungsgebiete

Aufgrund der weitgehenden Sprachneutralität kann dieser Algorithmus in folgenden Gebieten angewandt werden:

• Rechtschreibkorrektur (für Korrekturvorschläge)
• Suche nach ähnlichen Schlüsselwörtern (Überwachung, Spracherkennung, …)
• Grundwortreduktion (Stemming) im Information Retrieval

Statistik

Als N-Gramm-Statistik bezeichnet man eine Statistik über die Häufigkeit von N-Grammen, manchmal auch von Wortkombinationen aus N Wörtern. Spezialfälle sind die Bigrammstatistik und die Trigrammstatistik. Anwendungen finden N-Gramm-Statistiken in der Kryptoanalyse und in der Linguistik, dort vor allem bei Spracherkennungssystemen. Dabei prüft das System während der Erkennung die verschiedenen Hypothesen zusammen mit dem Kontext und kann dadurch Homophone unterscheiden. In der Quantitativen Linguistik interessiert unter anderem die Rangordnung der N-Gramme nach Häufigkeit sowie die Frage, welchen Gesetzen sie folgt. Eine Statistik von Digrammen (und Trigrammen) im Deutschen, Englischen und Spanischen findet man bei Meier^[1] und Beutelsbacher.^[2]

Für aussagefähige Statistiken sollten ausreichend große Textbasen von mehreren Millionen Buchstaben oder Wörtern benutzt werden. Als Beispiel ergibt die statistische Auswertung einer deutschen Textbasis von etwa acht Millionen Buchstaben „ICH“ als das häufigste Trigramm mit einer relativen Häufigkeit von 1,15 Prozent. Die folgende Tabelle gibt eine Übersicht über die zehn (in dieser Textbasis) als häufigste ermittelten Trigramme:

Trigramm	Häufigkeit
ICH	1,15 %
EIN	1,08 %
UND	1,05 %
DER	0,97 %
NDE	0,83 %
SCH	0,65 %
DIE	0,64 %
DEN	0,62 %
END	0,60 %
CHT	0,60 %

Literatur

• Wolfgang Schönpflug: N-Gramm-Häufigkeiten in der deutschen Sprache. I. Monogramme und Digramme. In: Zeitschrift für experimentelle und angewandte Psychologie XVI, 1969, S. 157-183.

Einzelnachweise

1. ↑ Helmut Meier: Deutsche Sprachstatistik. Zweite erweiterte und verbesserte Auflage. Olms, Hildesheim 1967, S. 336-339
2. ↑ Albrecht Beutelspacher, Kryptologie, 7. Aufl., Wiesbaden: Vieweg Verlagsgesellschaft, 2005, ISBN 3-8348-0014-7, Seite 230-236; dabei auch: Trigramme.

Weblinks