NP-vollständig

Der Begriff NP-Vollständigkeit ist ein Begriff aus der Komplexitätstheorie der Theoretischen Informatik, der im Jahre 1971 von Stephen A. Cook durch den Satz von Cook eingeführt wurde. Er zeichnet spezielle formale Sprachen der Komplexitätsklasse NP aus. So werden solche Sprachen NP-vollständig genannt, die – intuitiv gesprochen – die vollständige Schwierigkeit aller Sprachen aus der Komplexitätsklasse NP in sich tragen.

Der Begriff benötigt eine Rechtfertigung in dem Sinn, dass überhaupt wenigstens eine derartige Sprache existiert. Die wesentliche Leistung von Cook bestand zunächst darin, diesen Nachweis erbracht zu haben. Heute existieren wesentlich einfachere Nachweise für die Existenz einer solchen Sprache, allerdings sind die dafür verwendeten Sprachen sehr künstlich. Cooks Verdienst besteht also auch darin, für eine besonders interessante Sprache diesen Nachweis erbracht zu haben.

Aufbauend auf der Arbeit von Cook konnte Richard Karp im Jahre 1972 eine weitere bahnbrechende Arbeit vorlegen, die der Theorie der NP-Vollständigkeit zu noch größerer Popularität verhalf. Karps Verdienst besteht darin, die Technik der Polynomialzeitreduktion konsequent genutzt zu haben, um für weitere 21 populäre Probleme die NP-Vollständigkeit nachzuweisen.

Die Bedeutung der gesamten Theorie begründet sich vor allem auf folgenden Eigenschaften NP-vollständiger Sprachen (siehe P-NP-Problem):

1. Es konnte bisher für keine dieser Sprachen nachgewiesen werden, dass ein Algorithmus existiert, der für ihr Wortproblem in polynomieller Zeit eine korrekte Antwort liefert.
2. Wenn für eine NP-vollständige Sprache ein Algorithmus gefunden wird, der in polynomieller Zeit eine korrekte Antwort liefert, dann kann das Wortproblem für alle Sprachen in der Komplexitätsklasse NP in polynomieller Zeit entschieden werden.

Seit der Einführung der NP-Vollständigkeit durch Cook wurde die Vollständigkeit zu einem allgemeinen Konzept für beliebige Komplexitätsklassen ausgebaut.

Definition

Ein Problem (genauer: ein Entscheidungsproblem) L heißt NP-vollständig genau dann, wenn:

• L in der Klasse NP liegt, das heißt 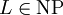$L \in {\rm NP}$ und
• L NP-schwierig ist, das heißt $\forall L' \in {\rm NP}: L' \preceq_{p} L$.

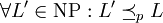Letztere Bedingung bedeutet, dass jedes Problem in NP durch eine Polynomialzeitreduktion auf L reduziert werden kann.

Nachweis der NP-Vollständigkeit

Der Nachweis der ersten Eigenschaft für ein Problem ist in aller Regel einfach. Man „rät“ eine Lösung und zeigt, dass man in Polynomialzeit verifizieren kann, ob die Lösung wirklich zutrifft. Im Raten der (korrekten) Lösung findet sich der Nichtdeterminismus wieder.

Der Nachweis der zweiten Eigenschaft, die man für sich allein mit NP-Schwierig (oder durch falsche Rück-Übersetzung aus englisch 'NP-hard' mit NP-Hart) bezeichnet, ist schwieriger. Insbesondere bereitet es Probleme, eine Aussage für beliebige Probleme in NP zu zeigen. Daher nimmt man gewöhnlich ein ähnliches Problem, für das die NP-Vollständigkeit schon bekannt ist, und reduziert es auf dasjenige Problem, für das die Eigenschaft der NP-Schwere gezeigt werden soll. Aus der Transitivität von Polynomialzeitreduktionen folgt dann, dass alle anderen Probleme aus NP ebenfalls auf das betrachtete Problem reduzierbar sind.

Die obige Definition erfordert streng genommen einen Existenzbeweis. Es ist nicht sofort ersichtlich, dass derartige Probleme überhaupt existieren. Es lässt sich aber leicht ein solches Problem konstruieren. Allerdings ist ein derart konstruiertes Problem kaum praxisrelevant. Cook konnte jedoch zeigen, dass das Erfüllbarkeitsproblem der Aussagenlogik NP-vollständig ist, und hat damit für ein praxisrelevantes Problem den Nachweis geführt. Dieser Beweis konnte im Gegensatz zu anderen Problemen natürlich noch nicht wie oben dargestellt über die Transitivität von Polynomialzeitreduktionen geführt werden und musste direkt erfolgen.

NP-Äquivalenz

Der Begriff NP-Vollständigkeit ist nur für Entscheidungsprobleme definiert, also solche Probleme, die sich auf das Wortproblem einer formalen Sprache zurückführen lassen, für die als Antwort also nur entweder Ja oder Nein in Frage kommt. Für Optimierungsprobleme und Suchprobleme gibt es den Begriff der NP-Äquivalenz.

Approximation

Probleme, die in NP liegen, lassen sich weiter in ihrer Komplexität unterteilen, je nach dem, wie gut sie sich approximativ lösen lassen. Das Graphen-Färbungsproblem ist beispielsweise nur sehr schlecht approximierbar, während sich andere Probleme beliebig gut mittels so genannter Approximationsschemata approximieren lassen.

Starke und schwache NP-Vollständigkeit

Die NP-vollständigen Probleme können weiterhin eingeteilt werden in

• stark NP-vollständige und
• schwach NP-vollständige Probleme

Ein NP-vollständiges Problem heißt stark NP-vollständig, falls es auch dann noch NP-vollständig ist, wenn die Eingabe nur aus Zahlen besteht, deren Größe im Verhältnis zur Eingabelänge polynomiell beschränkt ist. Andernfalls heißt das Problem schwach NP-vollständig. Schwache NP-Vollständigkeit bedeutet, dass für entsprechende Probleme pseudopolynomielle Algorithmen existieren können. Dies sind Algorithmen, deren Laufzeit polynomiell ist, wenn die Größe aller in der Eingabe vorkommenden Zahlen polynomiell in der Eingabelänge beschränkt ist. Für stark NP-vollständige Probleme gibt es – unter der Annahme NP ungleich P – keine derartigen Algorithmen.

Ein Beispiel für ein Problem, für das ein pseudopolynomieller Algorithmus existiert, ist das Rucksackproblem^[1]. Durch Algorithmen, die auf dem Prinzip der dynamischen Programmierung basieren, kann eine Laufzeit, die mit O(n*V) beschränkt ist, erreicht werden. Die Rechenzeit ist somit polynomiell, falls die Zahl V (die Schranke für den maximal erlaubten Nutzwert) im Verhältnis zur Eingabelänge n nur polynomiell groß ist.

Quellen

1. ↑ Siehe Seite 73 in dem Buch "Approximationsalgorithmen eine Einführung" von Rolf Wanka, Veröffentlicht von Vieweg+Teubner Verlag, 2006, ISBN 3519004445, ISBN 9783519004448, 206 Seiten

Literatur

• Michael R. Garey und David S. Johnson: Computers and Intractability: A Guide to the Theory of NP-Completeness. Freeman, San Francisco 1978, ISBN 0716710455
• Stephen A. Cook: The Complexity of Theorem Proving Procedures. In Annual ACM Symposium on Theory of Computing (STOC), pp 151--158, 1971. (pdf.gz)

Weblinks

• NPC (NP-Complete) im Complexity Zoo (englisch)
• Compendium of NP-complete optimization problems (englisch)
• Graph of NP-complete Problems (englisch)