- Nerode Relation
-
Die Nerode-Relation (auch: Nerode-Kongruenz oder Nerode-Rechtskongruenz) ist eine Äquivalenzrelation, die im Wissensgebiet Formale Sprachen der Theoretischen Informatik zum Einsatz kommt. Sie teilt die Präfixe von Wörtern einer formalen Sprache in Äquivalenzklassen auf.
Inhaltsverzeichnis
Definition
Gegeben sei eine Sprache L über dem Alphabet Σ. Die Nerode-Relation ~ (auch:
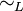 ) ist definiert durch:
) ist definiert durch:- Zwei Wörter sind bezüglich der Nerode-Relation genau dann äquivalent zueinander, wenn sie beide durch exakt dieselben Suffixe zu Wörtern der Sprache L ergänzt werden.
Formal gilt also für alle x, y aus Σ*:
Äquivalenzklasse
Die Äquivalenzklasse [x] einer Nerode-Relation für ein x aus Σ* ist definiert als Menge aller Wörter y aus Σ* welche bezüglich der Nerode-Relation äquivalent sind. Es gilt also:
Index
Der Index einer Nerode-Relation ist die Anzahl der vorhandenen Äquivalenzklassen.
Beispiel
Gegeben sei die durch den regulären Ausdruck
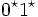 definierte Sprache. So enthält diese genau 3 Äquivalenzklassen:
definierte Sprache. So enthält diese genau 3 Äquivalenzklassen:- Die Äquivalenzklasse [0] enthält alle Präfixe welche aus Folgen von Nullen oder dem leeren Wort ε bestehen (also 0 * ).
- Die Äquivalenzklasse [1] besteht aus Wörtern, die mit 0en beginnen und mit 1en enden (also
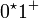 ), und zu guter Letzt
), und zu guter Letzt - [10], welche aus allen illegalen Präfixen besteht, das sind alle Wörter, die 10 enthalten (also {0,1} * 10{0,1} * ).
Weitere Beispiele finden sich in dem Artikel über den Satz von Myhill-Nerode.
Anwendung
Die Nerode-Relation bildet den Ausgangspunkt für den Satz von Myhill-Nerode, mit dem sich bestimmen lässt, ob eine Sprache regulär ist oder nicht. Sie wird außerdem verwendet, um zu einer gegebenen Sprache L einen minimalen Deterministischen endlichen Automaten zu konstruieren, also einen Automaten, der möglichst wenige Zustände besitzt. Ein solcher Automat enthält exakt ind(L) Zustände.
Wikimedia Foundation.

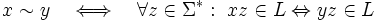
![[x] = \{ y \in \Sigma^\star | x \sim y \}](/pictures/dewiki/98/b2727804c3f24cf88994d64fbeb6f27c.png)