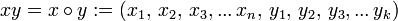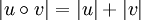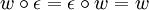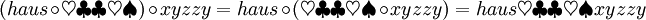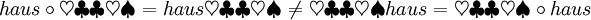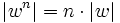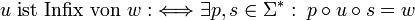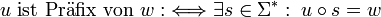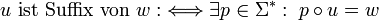- Suffix (Theoretische Informatik)
-
In der theoretischen Informatik ist ein Wort eine endliche Folge von Symbolen (Zeichenkette) aus einem Alphabet. Die Anzahl der Symbole eines Wortes w ist ihre Länge und wird mit | w | bezeichnet. Ein besonderes Wort ist das leere Wort, welches aus keinem Symbol besteht (die Länge 0 besitzt) und meist mit dem griechischen Buchstaben ε (Epsilon) dargestellt wird. Die Menge aller Wörter, welche man aus einem Alphabet Σ bilden kann, wird die Kleenesche Hülle über dieses Alphabet genannt und mit Σ * bezeichnet. Wörter bilden die Elemente einer formalen Sprache, welche als eine Teilmenge der Kleeneschen Hülle über ein gegebenes Alphabet definiert ist.
Inhaltsverzeichnis
Definition
Es sei Σ ein gegebenes Alphabet und n eine natürliche Zahl mit
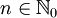 , wobei
, wobei 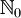 die Menge der natürlichen Zahlen einschließlich der Null bezeichnet
die Menge der natürlichen Zahlen einschließlich der Null bezeichnet 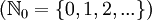 . Ein Wort w ist eine endliche Folge
. Ein Wort w ist eine endliche Folge 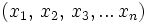 mit
mit 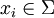 für alle
für alle 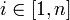 . Wie bereits erwähnt, ist die Zahl n die Länge des Wortes w.
. Wie bereits erwähnt, ist die Zahl n die Länge des Wortes w.Dabei wird zur Definition eines Wortes oft die vereinfachte Schreibweise
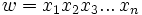 benutzt, was jedoch nur möglich ist, wenn das verwendete Alphabet eine eindeutige Zuordnung der benutzten Symbole zulässt. So kann diese Kurzschreibweise beim Alphabet
benutzt, was jedoch nur möglich ist, wenn das verwendete Alphabet eine eindeutige Zuordnung der benutzten Symbole zulässt. So kann diese Kurzschreibweise beim Alphabet 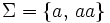 nicht angewendet werden, da hier zum Beispiel aus der Schreibweise w = aaa nicht eindeutig hervorgeht, ob das Wort
nicht angewendet werden, da hier zum Beispiel aus der Schreibweise w = aaa nicht eindeutig hervorgeht, ob das Wort 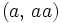 ,
, 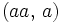 oder
oder 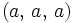 gemeint ist.
gemeint ist.Beispiele
Es seien mit Σ1 und Σ2 zwei Alphabete gegeben, wobei Σ1 das Alphabet der lateinischen Buchstaben und
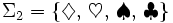 ist. Dann sind die Wörter w1 = haus und w2 = xyzzy Beispiele für Wörter über Σ1 und
ist. Dann sind die Wörter w1 = haus und w2 = xyzzy Beispiele für Wörter über Σ1 und 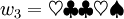 ist ein Wort über Σ2. Man erkennt, dass | w1 | = 4 und | w2 | = | w3 | = 5 ist.
ist ein Wort über Σ2. Man erkennt, dass | w1 | = 4 und | w2 | = | w3 | = 5 ist.Operationen auf Wörtern
Konkatenation
Die Konkatenation oder Verkettung ist eine Verknüpfung zweier Wörter zu einem neuen Wort, welche sich aus dem Aneinanderhängen der beiden Symbolfolgen ergibt. Die Konkatenation der beiden Wörter x und y über ein Alphabet Σ wird mit xy oder
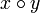 angegeben und ist definiert durch:
angegeben und ist definiert durch:Dabei ist nach der Definition des Wortes
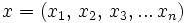 und
und 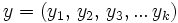 mit
mit 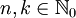 und
und 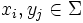 für alle
für alle 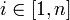 und
und 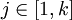 . Nach der obigen Definition ist x ein Prä- und y ein Suffix des durch die Konkatenation entstandenen Wortes
. Nach der obigen Definition ist x ein Prä- und y ein Suffix des durch die Konkatenation entstandenen Wortes 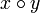 . Die Länge eines konkatenierten Wortes entspricht dabei der Summe aus den Längen der einzelnen (Teil-)Wörter. So gilt für jedes Wort u und v:
. Die Länge eines konkatenierten Wortes entspricht dabei der Summe aus den Längen der einzelnen (Teil-)Wörter. So gilt für jedes Wort u und v:Das neutrale Element der Konkatenation ist das leere Wort, da für jedes beliebige Wort w gilt, dass:
Somit bildet das Tripel der Menge aller Wörter über ein beliebiges Alphabet Σ, die Verknüpfung der Konkatenation und das leere Wort als neutrales Element einen Monoiden. Damit ist die Konkatenation assoziativ und es gilt zum Beispiel:
Demgegenüber ist die Konkatenation nicht kommutativ, d. h. nicht für alle Wörter u und v gilt, dass
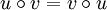 ist. Dies ist nämlich nur der Fall, wenn u und v übereinstimmen und/oder mindestens eines der beiden Wörter das leere Wort ist. So ist zum Beispiel:
ist. Dies ist nämlich nur der Fall, wenn u und v übereinstimmen und/oder mindestens eines der beiden Wörter das leere Wort ist. So ist zum Beispiel:Potenz
Die Potenz eines Wortes wn ist definiert als die n-fache Konkatenation dieses Wortes mit sich selbst. Die Definition der Potenz wird meist rekursiv angegeben:
- w0: = ε
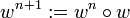 (für
(für 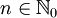 )
)
So sind zum Beispiel:
- xyzzy0 = ε
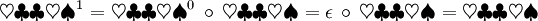
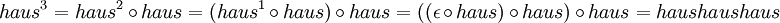
Nach der Definition der Konkatenation ist die Länge der n-fachen Potenz eines beliebigen Wortes w gleich dem Produkt aus n und der Länge von w:
Spiegelung
Die Spiegelung oder das Reverse wR eines Wortes w ist dasjenige Wort, welches sich ergibt, wenn man w rückwärts schreibt. Wenn also
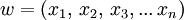 ist, so ist wR diejenige endliche Folge
ist, so ist wR diejenige endliche Folge 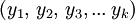 mit n = k und xi = yk − (i + 1) für alle
mit n = k und xi = yk − (i + 1) für alle 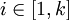 . Die Länge eines Wortes ist somit gleich der Länge seiner Spiegelung:
. Die Länge eines Wortes ist somit gleich der Länge seiner Spiegelung:- | wR | = | w |
So gilt zum Beispiel für die folgenden Wörter:
- εR = ε
- abbR = bba
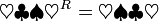
Das Reverse eines Wortes lässt sich außerdem mit Hilfe der strukturellen Induktion über dem Aufbau des betreffenden Wortes definieren. Dazu definiert man im Induktionsanfang, dass das Reverse des leeren Wortes gleich dem leeren Wort ist. Als Induktionsschritt definiert man, dass das Reverse eines aus einem Wort und einem Symbol zusammengesetzten Wortes gleich der Konkatenation des Symbols mit dem Reversen des Teilwortes ist:
Induktionsanfang:
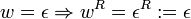
Induktionsschritt:
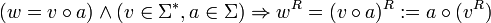
So lässt sich schrittweise das Reverse eines Wortes herleiten:
- εR = ε
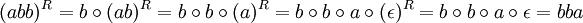
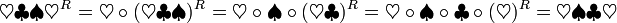
Ein Wort wie abaaba, welches identisch mit seiner Spiegelung ist, wird Palindrom genannt.
Infix, Suffix und Präfix
Infix
Jede endliche Teilfolge von aufeinander folgenden Symbolen eines Wortes w wird Infix oder Teilwort des Wortes w genannt. Ein Infix eines gegebenen Wortes
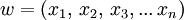 ist demnach jedes Wort
ist demnach jedes Wort 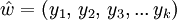 , für das es (mindestens) ein
, für das es (mindestens) ein 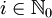 gibt, für welches gilt, dass zum einen
gibt, für welches gilt, dass zum einen 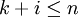 und zum anderen xj + i = yj für jedes
und zum anderen xj + i = yj für jedes 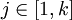 ist. Demnach ist ein Wort u genau dann Infix eines Wortes w, wenn gilt, dass es mindestens ein Wort p und s aus der Kleeneschen Hülle über dem Alphabet von w gibt, so dass
ist. Demnach ist ein Wort u genau dann Infix eines Wortes w, wenn gilt, dass es mindestens ein Wort p und s aus der Kleeneschen Hülle über dem Alphabet von w gibt, so dass 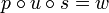 ist:
ist:So ist das Wort
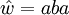 mit
mit 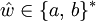 ein Infix der Wörter babaab, abaababb und aba, nicht aber der Wörter abba, babbaabbab beziehungsweise des leeren Wortes ε.
ein Infix der Wörter babaab, abaababb und aba, nicht aber der Wörter abba, babbaabbab beziehungsweise des leeren Wortes ε.Im Speziellen ist das leere Wort stets ein Infix jedes beliebigen Wortes und jedes Wort ist ein Infix von sich selbst. Ein Infix eines beliebigen Wortes, welches nicht identisch mit diesem ist, wird echtes Infix genannt.
Präfix
Ein Präfix eines Wortes ist ein Infix beliebiger Länge von aufeinander folgenden, führenden Symbolen dieses Wortes. Ein Präfix eines Wortes
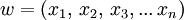 ist demnach jenes Infix
ist demnach jenes Infix 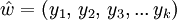 , für welches gilt, dass
, für welches gilt, dass 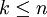 und xj = yj für jedes
und xj = yj für jedes 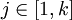 ist. Demnach ist u genau dann Präfix des Wortes w, wenn es mindestens ein s aus der Kleeneschen Hülle über dem Alphabet, aus dem w erzeugt wurde, gibt, so dass
ist. Demnach ist u genau dann Präfix des Wortes w, wenn es mindestens ein s aus der Kleeneschen Hülle über dem Alphabet, aus dem w erzeugt wurde, gibt, so dass 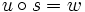 ist:
ist:So sind die Wörter ε, ab und abaab Präfixe des Wortes abaabb. Auch für Präfixe gilt, dass jedes Wort ein Präfix von sich selbst und das leere Wort stets ein Präfix jedes beliebigen Wortes ist. Echte Präfixe sind Präfixe eines Wortes, welche nicht identisch mit diesem Wort sind.
Suffix
Ein Suffix eines Wortes ist ein Infix beliebiger Länge von aufeinander folgenden Symbolen am Ende dieses Wortes. Ein Suffix eines Wortes
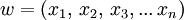 ist nach der Definition des Infixes jenes Teilwort
ist nach der Definition des Infixes jenes Teilwort 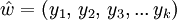 , für welches gilt, dass es ein
, für welches gilt, dass es ein 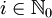 gibt, für das zum einen k + i = n und zum anderen xj + i = yj für jedes
gibt, für das zum einen k + i = n und zum anderen xj + i = yj für jedes 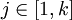 ist. Demnach ist ein Wort u genau dann Suffix eines Wortes w mit
ist. Demnach ist ein Wort u genau dann Suffix eines Wortes w mit 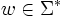 , wenn es mindestens ein
, wenn es mindestens ein 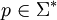 gibt, so dass
gibt, so dass 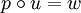 ist:
ist:So sind die Wörter ε, ab und abaab Suffixe des Wortes babaab. Wie für Präfixe und Infixe gilt auch für Suffixe, dass das leere Wort immer ein Suffix jedes beliebigen Wortes und ein beliebiges Wort stets auch ein Suffix von sich selbst ist. Ein Suffix eines Wortes, das nicht identisch mit ihm ist, wird echtes Suffix genannt.
Literatur
- John E. Hopcroft, Jeffry D. Ullman: Einführung in die Automatentheorie, formale Sprachen und Komplexitätstheorie. Bonn 1994, ISBN 3-89319-744-3.
- Katrin Erk, Lutz Priese: Theoretische Informatik: eine umfassende Einführung. 2., erw. Auflage. Springer-Verlag, 2002, ISBN 3-540-42624-8, S. 27–28.
- Gottfried Vossen, Kurt-Ulrich Witt: Grundkurs theoretische Informatik. Vieweg, 2006, ISBN 3834801534, S. 15 (online).
Weblinks
Wikimedia Foundation.