Nominales Merkmal

Die Nominalskala ist eines der Skalenniveaus in der Statistik. Ein Merkmal heißt nominal (v. lat. nomen „Name“ aus griech. onoma; Pl.: Nomina, auch Nomen), wenn seine möglichen Ausprägungen zwar unterschieden, nicht aber in eine Rangfolge gebracht werden können. Bei nominalskalierten Merkmalen wird der Untersuchungseinheit für die entsprechende Ausprägung (genau) ein Name bzw. (genau) eine Kategorie zugeordnet. Das Zuordnen von Zahlen zu den Elementen nennt man hier Nummerieren. Elemente derselben Kategorie bekommen dieselbe Nummer. Alle verwendeten Nummern bilden dann zusammen die sogenannte Nominalskala.

Die Nominalskala ordnet genau wie andere Skalen einem empirischen Relativ Zahlen zu. Die einzig zulässige Schlussfolgerung aus einer Nominalskala lautet: Gleiche Zahlen bedeuten gleiche Merkmalsausprägungen, unterschiedliche Zahlen bedeuten unterschiedliche Merkmalsausprägungen.

Zu den formalen Bedingungen einer Nominalskala gehören:

1. Reflexivität
   Formal geschrieben: a = a. Wenn ich z. B. einen Apfel vor mir habe und diesen als "Apfel" bezeichne (also der Merkmalsausprägung "Apfel" zuordne), dann sind alle Gegenstände, die ebenfalls diese Bezeichnung tragen, identisch.^[1]
2. Symmetrie
   Wenn a = b, dann ist b = a. Wenn ich das Bild eines Apfels sehe und ein ebensolches Objekt in meinen Händen halte, dann bezeichne ich dieses auch als "Apfel". Symmetrie ist dann gegeben, wenn das Beispiel umgedreht werden kann: Ich halte einen Apfel in der Hand und sehe ein Bild von einem gleichen Objekt und nenne das Objekt auf dem Bild auch "Apfel".
3. Transitivität
   Wenn a = b und b = c, dann ist a = c. Ich halte einen Apfel in der Hand, sehe ein Bild von einem Apfel und bezeichne beide als "Apfel" (a = b). Dann sehe ich das Bild mit dem Apfel, einen Apfel draußen an einem Baum hängen und bezeichne beide als "Apfel" (b = c). Dann muss ich auch wenn ich den Apfel in der Hand halte (a) und den Apfel draußen am Baum sehe (c) beide als "Apfel" bezeichnen (a = c).

Beispiele

Nachfolgende Tabelle enthält Beispiele für nominalskalierte Merkmale.

Merkmal	Kategorien
Geschlecht	männlich, weiblich
Beruf	Bäcker, Schuster, Tischler
Haarfarbe	braun, schwarz, rotblond, blond
Geburtsort	Hamburg, Berlin, München
Religionszugehörigkeit	evangelisch, katholisch, muslimisch
Hobbys	Schach, Tanzen, Angeln
Kleidung	Anzug, Rock, Kleid

Mögliche Operationen

Auch wenn einzelne Kategorien durch Zahlen kodiert werden sollten (Beruf 1, Beruf 2, ...), sind mathematische Operationen mit diesen Zahlen nicht sinnvoll, da sie keinen numerischen Wert sondern eine Kategorie (z. B. Tischler) darstellen. So ist beispielsweise eine Division "Tischler / Bäcker" wenig sinnvoll. Ebenso sind Größenvergleiche mittels nominalskalierter Merkmale nicht sinnvoll.

Möglich ist das Bestimmen von Auftrittshäufigkeiten der Kategorien in einer Menge von Untersuchungsobjekten.

Erlaubte Transformationen

Möglich sind sämtliche Transformationen, in der eine Kategorie ein-eindeutig einer anderen Kategorie zugeordnet ist. Zum Beispiel Umbenennen oder Permutationen (Veränderte Reihenfolge).

mathematische Deutung

Aus mathematischer Sicht ist eine Nominalskala S eine Menge, für die folgendes gilt:

1. Es existiert eine Äquivalenzrelation 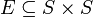$E \subseteq S \times S$, nämlich die Identitätsrelation auf S: $E = id_S = \left\{ \left(m,m\right) \vert m \in S \right\}$.

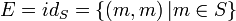Jedes Element 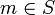$m \in S$ heißt Ausprägung von S.

Siehe auch

• Ordinalskala
• Kardinalskala

Einzelnachweise

1. ↑ Fritz Mauthner: Wörterbuch der Philosophie

Skalenniveaus

Nominalskala | Ordinalskala | Intervallskala | Verhältnisskala | Absolutskala