Octree

Ein Octree (von lat. octo „acht“, und engl. tree „Baum“) ist eine Datenstruktur der Informatik. Ein Octree ist ein gewurzelter Baum, dessen Knoten jeweils entweder acht direkte Nachfolger oder gar keine Nachfolger haben.

Octrees werden hauptsächlich in der Computergrafik verwendet, um dreidimensionale Datensätze hierarchisch zu untergliedern. Die Wurzel repräsentiert dabei alle Daten, jeder andere Knoten repräsentiert einen Oktanten der Daten seines direkten Vorgängers. Sie eignen sich dadurch zur Umsetzung der Strategie Teile und herrsche.

Octrees können als Erweiterung von Binärbäumen und Quadtrees angesehen werden: Binärbäume untergliedern eindimensionale Daten, Quadtrees zweidimensionale und Octrees dreidimensionale; gelegentlich wird eine Verallgemeinerung auf beliebig-dimensionale Daten N-Tree genannt. Eine weiter verallgemeinerte Version, bei der die Dimensionen nicht festgelegt sind, ist der B-Baum.

Anwendung

Schema eines Octrees. Links die Unterteilung des würfelförmigen Volumens, rechts der resultierende Octree.

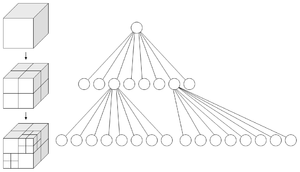
Das folgende Beispiel veranschaulicht die häufigste Anwendung eines Octrees, nämlich zur gleichmäßigen Gliederung eines würfelförmigen Datensatzes: Die Wurzel steht für den gesamten Würfel. Der Würfel wird in acht kleinere Würfel – die Oktanten – zerteilt und jeder Nachfolger der Wurzel steht für einen davon. Jeder dieser kleineren Würfel wird wiederum in acht noch kleinere Würfel zerteilt und so weiter. Die Untergliederung eines Teilwürfels endet, wenn keine weitere Teilung mehr möglich oder aber nicht notwendig ist.

Das Ursprungsvolumen muss nicht würfelförmig sein, sondern kann auch allgemein quaderförmig sein. Auch eine Unterteilung der Volumen in ungleich große Teile ist möglich. In der Regel werden in den Knoten zusätzliche Informationen über die untergeordneten Knoten abgelegt. So enthält z. B. jeder Knoten der speziellen Ausprägung Min-Max-Octree das Minimum und das Maximum des folgenden Teilbaumes, was effizientes Suchen ermöglicht.

Weitere Anwendungsgebiete

Allgemeine Anwendungsgebiete für Octrees sind:

• Bildrepräsentation
• Raumindizierung (z. B. in Geografischen Informationssystemen)
• Gruppierung von Partikeln in Molekulardynamik/DEM-Simulationen
• Hidden Surface Removal von Terraindaten.
• Kollisionserkennung in 3D-Computerspielen
• Hierarchical Splatting
• Zustandsschätzung^[1]

Spezielle Formen

Empty-Non-Empty-Octree

In einem Empty-Non-Empty-Octree wird in jedem Knoten entweder der Wert leer oder nicht-leer abgelegt. Leer gibt an, dass die vom Knoten repräsentierte Datenmenge keine verarbeitenswerten Daten enthält, nicht-leer gibt entsprechend an, dass die zugehörige Datenmenge verarbeitet werden muss. Leer ist normalerweise gleichzeitig das Abbruchkriterium für die Unterteilung; da die zugehörige Datenmenge keine interessanten Informationen mehr enthält, lohnt es sich auch nicht, sie weiter zu untergliedern.

Min-Max-Octree

Schema eines Min-Max-Octrees. Jeder Knoten enthält Minimum (oben) und Maximum (unten) seines Unterbaums. Bei der Suche nach dem Wert 3 müssen nur die Datenmengen der gelb markierten Knoten durchsucht werden.

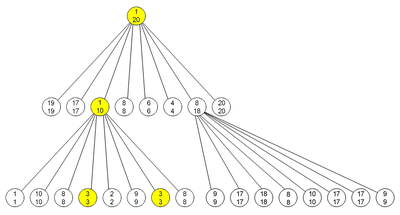
In einem Min-Max-Octree werden in jedem Knoten das Minimum und das Maximum des Unterbaums des Knotens abgelegt. Min-Max-Octrees eignen sich dadurch für effizientes Suchen nach dem Vorbild der Binärbäume. Der Unterbaum eines Knotens wird nur durchsucht, wenn der gesuchte Wert zwischen Minimum und Maximum des Knotens liegt. So können eventuell Teile des Baums ausgespart und die Suche dadurch beschleunigt werden.

Für den Spezialfall, dass Minimum und Maximum in einem Knoten gleich sind, kann die Suche im Unterbaum ebenfalls ausgespart werden, denn der gesamte Unterbaum des Knotens enthält den gesuchten Wert. Normalerweise ist der Fall Minimum gleich Maximum auch das Abbruchkriterium für die Unterteilung, das heißt die zugehörige Datenmenge wird nicht weiter untergliedert.

Min-Max-Octrees werden beispielsweise in der Volumengrafik zur Beschleunigung des Marching Cubes-Algorithmus verwendet. Hier werden alle Unterwürfel des Octrees gesucht, in denen ein vorgegebener Schwellwert enthalten ist. Dieser Schwellwert ist eine Materialdichte, für die aus den Voxeldaten eine Isooberfläche extrahiert werden soll.

Tensorfelder

Mathematisch betrachtet eignen sich Octrees besonders zur Gliederung von Tensorfeldern. Ein Voxelgitter mit Grauwerten beispielsweise ist als Skalarfeld ein Tensorfeld nullter Ordnung, Voxelgitter mit drei Farbwerten nach dem RGB-Schema und einer Alpha-Komponente sind als Vektorfeld ein Tensorfeld erster Ordnung.

Einzelnachweise

1. ↑ Henning Eberhardt, Vesa Klumpp, Uwe D. Hanebeck, Density Trees for Efficient Nonlinear State Estimation, Proceedings of the 13th International Conference on Information Fusion, Edinburgh, United Kingdom, July, 2010. (PDF-Datei; 3,2 MB)