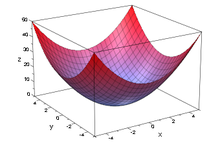
Skalarfeld

Skalarfeld x²+y²

In der mehrdimensionalen Analysis, der Vektorrechnung und der Differentialgeometrie ist ein Skalarfeld eine Funktion, die jedem Punkt eines Raumes eine reelle Zahl (Skalar) zuordnet. Skalarfelder sind von großer Bedeutung in der Feldbeschreibung der Physik, und in der mehrdimensionalen Vektoranalysis. Skalarfelder beschreiben zum Beispiel die Temperatur jedes Punktes in einem Raum.

Definition

Ein Skalarfeld liegt vor, wenn jeweils ein Skalar φ(P) zu einem Punkt P des Raumes ($\mathbb {R}^n$), oder einer Teilmenge von diesem, zugeordnet ist.

$P \in \mathbb {R}^n$

$\varphi:\ \mathbb{R}^n\rightarrow\mathbb{R}$

$P\mapsto\varphi(P)$

für n=3:

P = (x,y,z)

$\varphi:\ \mathbb{R}^3\rightarrow\mathbb{R}$

$P\mapsto\varphi(P)=\varphi(x,y,z)$

Beispiele

Beispiele für Skalarfelder in der Physik sind der Luftdruck, die Temperatur, Dichte oder allgemein Potentiale (auch als Skalarpotentiale bezeichnet). Potentiale mit expliziter Zeitabhängigkeit, z. B. V(x(t),y(t),z(t),t), sind dabei nicht  zugelassen, obwohl sie - nicht nur in der Mechanik - durchaus vorkommen. Allerdings ist dann die Energie-Erhaltung nicht erfüllt, sondern es wird von außen explizit Energie zugeführt

Operationen

Wichtige Operationen im Zusammenhang mit Skalarfeldern sind:

• Gradient eines Skalarfeldes, der ein Vektorfeld ist.
• Richtungsableitung eines Skalarfeldes.