Oktant (Geometrie)

In der Geometrie wird der dreidimensionale Raum durch die Koordinatenebenen eines kartesischen Koordinatensystems in 8 Teile zerlegt, die als Oktanten bezeichnet werden. Da die begrenzenden Koordinatenebenen in der Regel zu keinem Oktanten gehören, geben die jeweiligen Vorzeichen der Koordinaten eines Punktes im dreidimensionalen Raum an, in welchem der acht Oktanten ein Punkt liegt.

Nummerierung

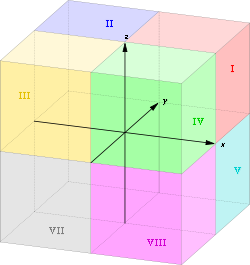
Der 1. Oktant (I) besteht aus allen Punkten, die drei positive Koordinaten haben. Im Bild rechts befindet er sich also oben hinten rechts. Die Oktanten II bis IV haben ebenfalls eine positive z-Koordinate, im Bild bleibt man also in der oberen Hälfte des Koordinatensystems, und zählt die Oktanten gegen den Uhrzeigersinn mit römischen Ziffern (I bis IV). Durch diese Festlegung ist gewährleistet, dass für die Oktanten I bis IV die gleichen Vorzeichen in den ersten beiden Koordinaten gelten wie für die Quadranten I bis IV in der Ebene. Entsprechend verfährt man in der unteren Hälfte (z < 0): Der 5. Oktant (V) befindet sich direkt unter dem 1. Oktanten. Auch hier zählt man weiter gegen den Uhrzeigersinn mit römischen Ziffern (V bis VIII).

Explizit ergeben sich also für die Oktanten folgende Vorzeichen der Koordinaten – die Reihenfolge der Koordinaten ist hierbei (x,y,z):

• I. Oktant: ( + , + , + )
• II. Oktant: ( − , + , + )
• III. Oktant: ( − , − , + )
• IV. Oktant: ( + , − , + )
• V. Oktant: ( + , + , − )
• VI. Oktant: ( − , + , − )
• VII. Oktant: ( − , − , − )
• VIII. Oktant: ( + , − , − )

Oktanten im zweidimensionalen Raum

Gelegentlich wird auch der zweidimensionale Raum in Oktanten unterteilt. Hierbei werden die vier Quadranten an den Geraden y = x und y = − x geteilt. Die so definierten Oktanten werden entgegen dem Uhrzeigersinn, beginnend mit der unteren Hälfte des I. Quadranten von I bis VIII durchnummeriert.

Siehe auch

• Orthant