- Koordinatenebene
-
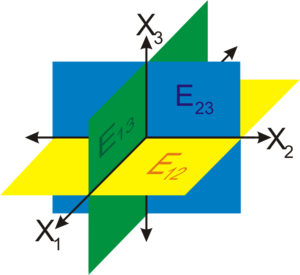
Als Koordinatenebenen bezeichnet man in der analytischen Geometrie die von jeweils zwei Einheitsvektoren aufgespannten Ursprungsebenen. Häufig tragen die Koordinatenebenen den Buchstaben E mit einem Index, der die Einheitsvektoren angibt, von denen die Ebene aufgespannt wird.
Im dreidimensionalen Raum
 gibt es genau drei Koordinatenebenen:
gibt es genau drei Koordinatenebenen:- E12, aufgespannt von
 und
und  ,
, - E13, aufgespannt von
 und
und  ,
, - E23, aufgespannt von
 und
und  ,
,
mit
 ,
,  und
und  .
.Koordinatenform der Koordinatenebenen
Im dreidimensionalen Raum haben die Koordinatenebenen folgende Gleichung in Koordinatenform:
Siehe auch
In der synthetischen Geometrie wird eine affine oder projektive Ebene, der als Koordinatenbereich eine Menge mit einer bestimmten algebraischen Struktur (ein Ternärkörper, Quasikörper, Alternativkörper, Schiefkörper etc.) zugeordnet werden kann, als Koordinatenebene über diesem verallgemeinerten Körper bezeichnet.
→ Siehe dazu Ternärkörper und Projektives Koordinatensystem.
- E12, aufgespannt von
Wikimedia Foundation.