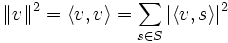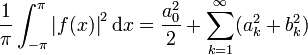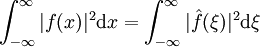Parseval'sche Gleichung

Die parsevalsche Gleichung (nach Marc-Antoine Parseval), auch bekannt als Abgeschlossenheitsrelation, aus dem Gebiet der Funktionalanalysis ist die allgemeine Form des Satzes des Pythagoras für Innenprodukträume. Zugleich ist sie wichtig für Orthogonalzerlegungen in diesen Räumen, insbesondere für die verallgemeinerte Fouriertransformation.

Formulierung

Es seien ein Innenproduktraum (Prähilbertraum) V und Orthonormalsystem S gegeben - d.h. alle Elemente von S sind zueinander orthogonal und haben zudem die Norm 1. S ist genau dann eine Orthonormalbasis von V, wenn für alle 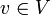$v \in V$ die parsevalsche Gleichung

$\|v\|^2=\langle v,v\rangle=\sum_{s\in S}|\langle v,s\rangle|^2$

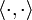erfüllt ist. Hierbei bezeichnet $\|\cdot\|$ die Norm und $\langle\cdot,\cdot\rangle$ das Innenprodukt.

Anwendungen

Die Gleichung hat die physikalische Aussage, dass die Energie eines Signals im Fourierraum betrachtet identisch zur Energie des Signals im Ortsraum ist.

Eine andere Formulierung der Gleichung ist die Aussage, dass die L²-Norm einer Funktion gleich der l2-Norm der Koeffizienten der Fourierreihe dieser Funktion ist. Die Verallgemeinerung der parsevalschen Gleichung auf die Fouriertransformation ist der Satz von Plancherel.

Spezialfall der Fourierreihe

Falls a_k,b_k die Fourierkoeffizienten der Fourierreihenentwicklung der (periodischen) Funktion f(x) sind, dann gilt die Gleichung

$\frac{1}{\pi} \int_{-\pi}^{\pi}\left|f(x)\right|^2 \mathrm dx = \frac{a_0^2}{2} + \sum_{k=1}^{\infty} (a_k^2 + b_k^2)$

Diese Identität ist ein Spezialfall der oben beschriebenen allgemeinen parsevalschen Gleichung, wenn man als Orthogonalsystem die trigonometrischen Funktionen 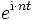$e^{\mathrm{i} \cdot nt}$ nimmt.

Satz von Plancherel

Der parsevalschen Gleichung für die Fourierreihe entspricht eine Identität der Fouriertransformation, die gemeinhin als Satz von Plancherel bezeichnet wird:

Falls 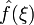$\hat{f}(\xi)$ die Fouriertransformierte von f(x) ist, dann gilt die Gleichung

$\int_{-\infty}^{\infty} |f(x)|^2 \mathrm dx = \int_{-\infty}^{\infty} |\hat{f}(\xi)|^2 \mathrm d \xi$

Die Fouriertransformation ist damit eine Isometrie im Hilbertraum L². Diese Gleichung ist der parsevalschen sehr ähnlich, aber sie folgt nicht aus dieser, da der Fouriertransformation kein Orthogonalsystem zugeordnet ist.

Literatur

• Dirk Werner: Funktionalanalysis, Springer-Verlag, Berlin, ISBN 978-3-540-72533-6