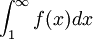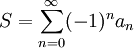- Partialsummenfolge
-
In der Mathematik ist eine (unendliche) Reihe eine Folge, deren Glieder (Partialsummen) als Summen der ersten n Glieder einer anderen Folge gegeben sind.
Inhaltsverzeichnis
Nomenklatur
Aus jeder Folge
 kann man eine Reihe
kann man eine Reihe  konstruieren mittels
konstruieren mittelsWir verwenden als Indizes für die Glieder von Folge und Reihe in diesem Artikel die natürlichen Zahlen einschließlich der Null; in manchen Anwendungen ist es üblich, die Null auszuschließen. Mit Hilfe des Summenzeichens können die einzelnen Glieder der Reihe auch abgekürzt als
geschrieben werden; sie werden auch Partialsummen der Folge (ai) genannt. Wenn (ai) und damit auch (sn) für alle nichtnegativen ganzen Indizes i bzw. n definiert sind, spricht man von einer unendlichen Reihe. Wenn der Grenzwert der Folge der Partialsummen
existiert, sagt man, die Reihe konvergiert; den Grenzwert S nennt man die Summe der Reihe oder den Wert der Reihe. Mit Hilfe des Summenzeichens kann diese Summe auch abgekürzt als
geschrieben werden.
Eine Reihe (sn) heißt divergent, wenn sie nicht konvergiert. Sie heißt bestimmt divergent oder uneigentlich konvergent, wenn die Teilsummen (sn) gegen -∞ oder +∞ streben. Andernfalls heißt die Reihe unbestimmt divergent; dabei kann sie Häufungspunkte haben oder auch nicht.
Mit verschiedenen Konvergenzkriterien lässt sich feststellen, ob eine Reihe konvergiert.
Beispiele
Für einige einfache endliche Reihen kann man die Summe explizit berechnen, beispielsweise für arithmetische Reihen wie
oder die Summe der ersten n Quadrate lautet
Ein Beweis solcher Formeln kann z. B. über vollständige Induktion erfolgen. Es gibt jedoch auch konstruktive Methoden, Reihen explizit zu summieren: Eulersche Summenformel, Teleskopsummen, Summation und Umordnung bekannter Reihen. Weitere solche Summationsformeln finden sich in der Formelsammlung Algebra.
Eine weitere klassische Reihe ist die geometrische Reihe, der Name ergibt sich aus der geometrischen Folge (an = qn für
 ). Die unendliche geometrische Reihe ist also:
). Die unendliche geometrische Reihe ist also:Weitere Beispiele endlicher Reihen findet man im Artikel Addition.
Eine spezielle geometrische Reihe ist
Diese Schreibweise bezeichnet nach der oben gegebenen Darstellung den Grenzwert der Folge
Man kann die Konvergenz dieser Reihe auf der Zahlengeraden visualisieren: Stellen wir uns eine Linie mit der Länge zwei vor, auf der aufeinanderfolgende Abschnitte mit den Längen 1, 1/2, 1/4, usw. markiert sind. Es gibt auf dieser Linie immer noch Platz für einen weiteren Abschnitt, da immer noch so viel Platz ist, wie der letzte Abschnitt lang war: Wenn wir die Strecke 1/2 markiert haben, haben wir insgesamt 3/2 verbraucht, es bleiben also noch 1/2 übrig. Wenn wir nun 1/4 wegstreichen, bleibt ein weiteres 1/4 übrig, etc. Da das „Reststück“ beliebig klein wird, ist der Grenzwert gleich 2.
Konvergente geometrische Reihen sind auch ein Gegenstand der Paradoxa von Zenon.
Ein Beispiel für eine divergente Reihe mit mehreren Häufungspunkten ist die Summe über die Folge +1,-1,+1,-1,… Die Reihe wechselt zwischen den Werten 1 und 0 (die Folge hingegen wechselt zwischen 1 und −1).
Konvergenzkriterien
Im Folgenden seien die Zahlen an stets reelle oder komplexe Zahlen, und die Reihe S definiert als
Zum Beweis der Konvergenz dieser Reihe gibt es diverse Konvergenzkritierien, die teils die bedingte, teils die stärkere absolute Konvergenz zeigen:
- Notwendige Bedingung
Wenn die Reihe S konvergiert, dann konvergiert die Folge (an) der Summanden gegen 0 für
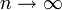 . Die Umkehrung ist nicht allgemeingültig (ein Gegenbeispiel ist die harmonische Reihe).
. Die Umkehrung ist nicht allgemeingültig (ein Gegenbeispiel ist die harmonische Reihe).Wenn alle Glieder an der Reihe S nichtnegative reelle Zahlen sind, S konvergiert und für alle n
mit reellen oder komplexen Zahlen bn gilt, dann konvergiert auch die Reihe
absolut, und es ist |T| ≤ S.
Wenn alle Glieder an der Reihe S nichtnegative reelle Zahlen sind, S divergiert und für alle n gilt
mit nichtnegativen reellen Zahlen bn gilt, dann divergiert auch die Reihe
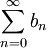 .
.
Wenn eine Konstante C < 1 und ein Index N existiert, sodass für alle n ≥ N gilt
dann konvergiert die Reihe S absolut.
Wenn eine Konstante C < 1 und ein Index N existiert, sodass für alle n ≥ N gilt
dann konvergiert die Reihe S absolut.
Ist
![f: [1, \infty] \to [0, \infty]](/pictures/dewiki/57/932cfc3523707160d60b5d3a4f5992da.png) eine nichtnegative, monoton fallende Funktion mit
eine nichtnegative, monoton fallende Funktion mit- f(n) = an für alle n,
dann konvergiert S genau dann, wenn das Integral
existiert.
Eine Reihe der Form
mit nichtnegativen an wird alternierende Reihe genannt. Eine solche Reihe konvergiert, wenn die Folge an monoton gegen 0 konvergiert. Die Umkehrung ist nicht allgemeingültig.
Beispiele
- Eine geometrische Reihe
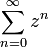 konvergiert genau dann, wenn | z | < 1.
konvergiert genau dann, wenn | z | < 1.
- Die Reihe
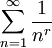 konvergiert, wenn r > 1 und divergiert für
konvergiert, wenn r > 1 und divergiert für 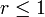 , was mit dem Integralkriterium gezeigt werden kann. Als Funktion von r aufgefasst, ergibt diese Reihe die Riemannsche Zetafunktion.
, was mit dem Integralkriterium gezeigt werden kann. Als Funktion von r aufgefasst, ergibt diese Reihe die Riemannsche Zetafunktion.
- Die Teleskopreihe
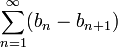 konvergiert genau dann, wenn die Folge bn für
konvergiert genau dann, wenn die Folge bn für 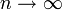 gegen eine Zahl L konvergiert. Der Wert der Reihe ist dann b1 − L.
gegen eine Zahl L konvergiert. Der Wert der Reihe ist dann b1 − L.
Reihen von Funktionen
Anstatt Folgen von Zahlen kann man auch Folgen von Funktionen betrachten und entsprechend Reihen definieren. Hier kommt zur Frage der Konvergenz noch die nach den Eigenschaften der Grenzfunktion hinzu. Umgekehrt kann man fragen, durch welche Reihe sich eine Funktion darstellen lässt. So eine Darstellung nennt sich Reihenentwicklung.
Potenzreihen
Einige wichtige Funktionen können als Taylorreihen dargestellt werden. Diese sind bestimmte unendliche Reihen, in denen Potenzen einer unabhängigen Variable vorkommen. Solche Reihen werden allgemein Potenzreihen genannt. Werden auch negative Potenzen der Variablen zugelassen, spricht man von Laurentreihen.
Fourierreihen
Als Fourierreihe einer Funktion bezeichnet man ihre Entwicklung nach trigonometrischen Funktionen sin(nx) und cos(nx) (n = 0,1,2,3,...).
Dirichletreihen
Als Dirichletreihe bezeichnet man eine Entwicklung
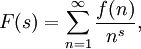 mit
mit 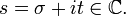
Ein wichtiges Beispiel ist die Riemannsche Zetafunktion
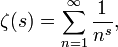 mit
mit 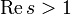 .
.
Literatur
- K. Knopp: Theorie und Anwendung der unendlichen Reihen. Berlin 1996. ISBN 3-540-59111-7
Wikimedia Foundation.

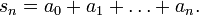
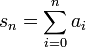
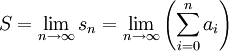
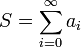
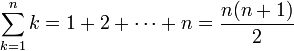
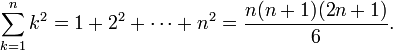
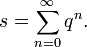

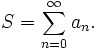
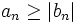
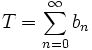
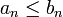
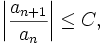
![\sqrt[n]{|a_n|} \le C,](/pictures/dewiki/50/2e667f75c58bdb56131b8181c1dbedc8.png)