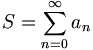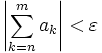Cauchy-Eigenschaft — Das Cauchykriterium für unendliche Reihen (nach Augustin Louis Cauchy) ist ein mathematisches Konvergenzkriterium, also ein Mittel zur Entscheidung ob eine unendliche Reihe konvergent oder divergent ist. Sei eine unendliche Reihe mit reellen oder … Deutsch Wikipedia
Cauchy-Riemannsche partielle Differentialgleichungen — Die Cauchy Riemannschen partiellen Differentialgleichungen (nach Augustin Louis Cauchy und Bernhard Riemann) sind ein Begriff aus der Funktionentheorie und ein Kriterium für komplexe Differenzierbarkeit. Die Gleichungen wurden das erste Mal 1814… … Deutsch Wikipedia
Cauchy-Filter — Uniforme Räume im Teilgebiet Topologie der Mathematik sind Verallgemeinerungen von metrischen Räumen. Jeder metrische Raum kann auf natürliche Weise als uniformer Raum betrachtet werden, und jeder uniforme Raum kann auf natürliche Weise als… … Deutsch Wikipedia
Cauchy-Riemann-Differentialgleichungen — Die Cauchy Riemann schen partiellen Differentialgleichungen (nach Augustin Louis Cauchy und Bernhard Riemann) sind ein Begriff aus der Funktionentheorie und ein Kriterium für komplexe Differenzierbarkeit. Die Gleichungen wurden das erste Mal 1814 … Deutsch Wikipedia
Cauchy-Riemann-Gleichungen — Die Cauchy Riemann schen partiellen Differentialgleichungen (nach Augustin Louis Cauchy und Bernhard Riemann) sind ein Begriff aus der Funktionentheorie und ein Kriterium für komplexe Differenzierbarkeit. Die Gleichungen wurden das erste Mal 1814 … Deutsch Wikipedia
Cauchy-Riemannsche Differentialgleichungen — Die Cauchy Riemann schen partiellen Differentialgleichungen (nach Augustin Louis Cauchy und Bernhard Riemann) sind ein Begriff aus der Funktionentheorie und ein Kriterium für komplexe Differenzierbarkeit. Die Gleichungen wurden das erste Mal 1814 … Deutsch Wikipedia
Cauchy-Problem — Als Anfangswertproblem (AWP) (manchmal auch als Anfangswertaufgabe (AWA) oder Cauchy Problem genannt) bezeichnet man in der Analysis eine wichtige Klasse von Differentialgleichungen, bei denen aus vorgegebenen Anfangsdaten, nämlich dem… … Deutsch Wikipedia
Cauchy'sches Verdichtungskriterium — Das Cauchysche Verdichtungskriterium, auch bekannt als Cauchyscher Verdichtungssatz (nach Augustin Louis Cauchy), ist ein mathematisches Konvergenzkriterium, also ein Mittel zur Entscheidung, ob eine unendliche Reihe konvergent oder divergent ist … Deutsch Wikipedia
Augustin Louis Cauchy — [ogysˈtɛ̃ lwi koˈʃi] (* 21. August 1789 in Paris; † 23. Mai 1857 in Sceaux) war ein französischer Ma … Deutsch Wikipedia
Epsilon-Delta-Kriterium — Die Stetigkeit ist ein Konzept der Mathematik, das vor allem in den Teilgebieten der Analysis und der Topologie von zentraler Bedeutung ist. Eine Funktion heißt stetig, wenn verschwindend kleine Änderungen des Argumentes (der Argumente) nur zu… … Deutsch Wikipedia
 ein Index N existiert, so dass für alle m und n mit m > n > N gilt:
ein Index N existiert, so dass für alle m und n mit m > n > N gilt: (bzw.
(bzw.  ). Ist das Kriterium nicht erfüllt, divergiert sie.
). Ist das Kriterium nicht erfüllt, divergiert sie. und
und  folgt dann die Konvergenz der Reihe.
folgt dann die Konvergenz der Reihe.