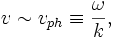Plasmaoszillationen

In der Physik ist eine Plasmaoszillation eine periodische Oszillation der Ladungsdichte in einem elektrisch leitenden Medium, zum Beispiel in einem Plasma oder einem Metall. Das Quasiteilchen, das aus der Quantisierung dieser Oszillationen hervorgeht, ist das Plasmon.

Ein Plasma besteht aus Ionen mit positiver Ladung und Elektronen mit negativer Ladung. Plasmen sind quasi-neutral, das heißt, positive und negative Ladungsdichte sind im Mittel gleich groß.

Plasmafrequenz

Werden die Elektronen gegenüber den Ionen z.B. durch eine elektromagnetische Welle leicht versetzt, wirkt auf sie die Coulombkraft, die die Quasi-Neutralität wieder herstellt. Durch ihre Trägheit werden die Elektronen an der neutralen Lage vorbeischießen und einen neuen Ladungsüberschuß aufbauen. Die Frequenz, mit der die Elektronen gegenüber den positiven Ionen schwingen heißt Plasmafrequenz:

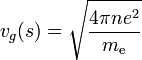$v_{g}(s) = \sqrt{ \frac{4 \pi n e^{2} }{ m_{\mathrm{e}} } }$ (CGS-Einheiten),

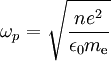$\omega_{p} = \sqrt{\frac{n e^{2}}{\epsilon_{0} m_{\mathrm{e}}}}$ (SI-Einheiten),

wobei n die Elektronendichte, e die Elementarladung, und m_e die Elektronenmasse ist.

Die Plasmafrequenz ergibt sich aus dem zweiten newtonschen Gesetz, wenn man die Bewegung eines Elektrons im Feld der als ruhend angenommenen Ionen betrachtet. Zur Herleitung kann der Einfachheit halber der eindimensionale Fall angenommen werden. Außerdem betrachten wir nur ein Wasserstoff-Plasma mit einfach geladenen Ionen. Das Feld der Ionen erhält man aus dem Gaußschen Gesetz mit der Ladungsdichte ρ = en_e und der eindimensionalen Divergenz 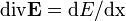$\mathrm{div} \mathbf{E} = \mathrm{d}E/\mathrm{dx}$ nach Integration zu E(x) = en_ex / ε₀. Die Bewegungsgleichung ist dann 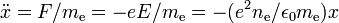$\ddot{x} = F/m_\mathrm{e} = -e E /m_\mathrm{e} = -(e^2 n_\mathrm{e}/\epsilon_0 m_\mathrm{e})x$. Dies ist die Bewegungsgleichung des harmonischen Oszillators, die durch eine harmonische Schwingung mit ω = ω_p gelöst wird.

Dispersionsrelation

Weil die Frequenz unabhängig von der Wellenlänge ist, haben Plasmaoszillationen eine unendliche Phasengeschwindigkeit und eine verschwindende Gruppengeschwindigkeit.

Wenn die Elektronen eine endliche thermische Geschwindigkeit 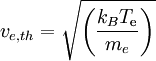$v_{e,th} = \sqrt{\left( \frac{k_B T_{\mathrm{e}}}{m_e} \right) }$ haben, wirkt der Elektronendruck zusätzlich zu dem elektrischen Feld als Rückstellkraft. Dann propagieren die Oszillationen mit der Bohm-Gross Dispersionsrelation

$\omega^2 = \omega_{pe}^2 + 3 k^2 v_{\mathrm{e,th}}^2$.

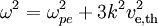Hier steht T_e für die auf die Elektronruhemasse m_e normierte Elektronentemperatur T. Wenn die räumliche Skala groß ist gegenüber der Debye-Länge, spielt der Druck eine untergeordnete Rolle. Auf kleinen Skalen dominiert der Druck und die Wellen werden dispersionslos mit der Geschwindigkeit 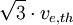$\sqrt{3} \cdot v_{e,th}$. Für solche Wellen aber ist die thermische Geschwindigkeit vergleichbar mit der Phasengeschwindigkeit

$v \sim v_{ph} \equiv \frac{\omega}{k},$

so dass die Plasmawelle einzelne Elektronen beschleunigen kann. Dieser Prozess ist eine Art kollisionslose Dämpfung, Landau-Dämpfung genannt. Aus dem Grund ist die Dispersionbeziehung bei großem k schwer zu beobachten und nur selten wichtig.

Anwendung der Plasmaoszillation

Elektronen mit einer bestimmten Plasmafrequenz können also fast instantan Bewegungen ausführen, die "langsamer" als die Plasmafrequenz ablaufen. Das heißt insbesondere, dass Plasmen elektromagnetische Wellen mit Frequenzen unterhalb der Plasmafrequenz fast vollständig reflektieren, für Wellen mit oberhalb der Plasmafrequenz liegenden Frequenzen hingegen transparent sind.

Reflexion von Licht an Metallen

Die Plasmafrequenz liegt in metallischen Festkörpern bei typischen Elektronendichten von n_e = 10²⁸m ^{− 3} im Bereich von 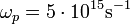$\omega_p=5\cdot10^{15}\mathrm{s}^{-1}$ was über die Dispersionsrelation für elektromagnetische Wellen einer Wellenlänge von 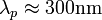$\lambda_p \approx 300 \mathrm{nm}$ entspricht. Metalle reflektieren deshalb Licht im optischen Bereich, für UV-Licht hingegen sind sie meist transparent.

Reflexion von Radiowellen an der Atmosphäre

Plasmaoszillationen in der Ionosphäre der Erde sind der Grund dafür, dass mit Kurzwellen ausgestrahlte Radioprogramme eine sehr große Reichweite besitzen. Die Radiowellen treffen auf die Ionosphäre auf und regen die Elektronen zum Schwingen an. Dies führt zu einer Reflexion der Welle an der Ionosphäre. Über Kurzwelle ausgesendete Programme können deshalb auch an Orten empfangen werden, die eigentlich im Sichtschatten des Senders liegen. Die maximale reflektierte Frequenz ist gerade die Plasmafrequenz. Daher ist zum Beispiel die Kommunikation mit Satelliten nur über noch höhere Frequenzen im UKW-Band möglich.

Siehe auch

• Raman-Streuung