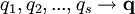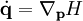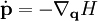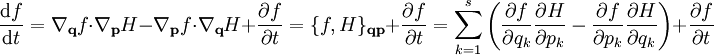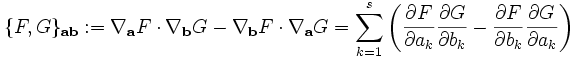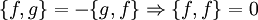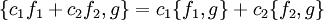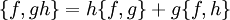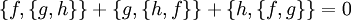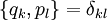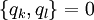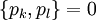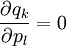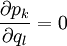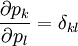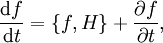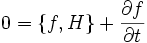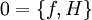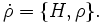Poisson-Klammer (klassische Mechanik)

Die Poisson-Klammer (nach Siméon Denis Poisson) ist ein bilinearer Differentialoperator in der kanonischen (hamiltonschen) Mechanik. Sie ist definiert als

$\left \{ f,g \right \} := \sum_{k=1}^{s}{\left ( \frac{\partial f}{\partial q_k} \frac{\partial g}{\partial p_k} - \frac{\partial f}{\partial p_k} \frac{\partial g}{\partial q_k} \right )},$

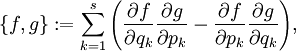
wobei f und g Funktionen sind. Hierbei sind die q_k die generalisierten Koordinaten, p_k die kanonisch konjugierten Impulse und s die Anzahl der Freiheitsgrade.

Herleitung

Der Einfachheit halber verwenden wir Vektorschreibweise

$q_1,q_2,...,q_s \rightarrow \mathbf{q}$

sowie

$p_1,p_2,...,p_s \rightarrow \mathbf{p}$.

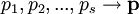Zudem verwenden wir bei den partiellen Ableitungen die vektorielle Notation mit einem Skalarprodukt im s-dimensionalen Raum, also etwa

$\sum^s_{k=1}\frac{\partial H}{\partial q_k} \dot q_k=\nabla_{\mathbf{q}}H \cdot \dot\mathbf{q}$,

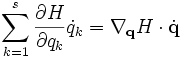wobei H die Hamilton-Funktion des Systems ist. Mit diesen Vereinfachungen wird die Zeitableitung einer beliebigen Observablen 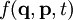$f(\mathbf{q},\mathbf{p},t)$ zu

$\frac{\mathrm{d}f}{\mathrm{d}t}=\nabla_{\mathbf{q}}f \cdot \dot\mathbf{q}+\nabla_{\mathbf{p}}f \cdot \dot\mathbf{p}+\frac{\partial f}{\partial t}$.

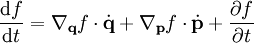Benutzen wir nun die Hamilton'schen Gleichungen in vektorieller Form,

$\dot\mathbf{q}=\nabla_{\mathbf{p}}H$

$\dot\mathbf{p}=-\nabla_{\mathbf{q}}H$

so erhalten wir damit

$\frac{\mathrm{d}f}{\mathrm{d}t}=\nabla_{\mathbf{q}}f \cdot \nabla_{\mathbf{p}}H-\nabla_{\mathbf{p}}f \cdot \nabla_{\mathbf{q}}H+\frac{\partial f}{\partial t}=\{f,H\}_{\mathbf{qp}} + \frac{\partial f}{\partial t}=\sum^s_{k=1}\left(\frac{\partial f}{\partial q_k}\frac{\partial H}{\partial p_k}-\frac{\partial f}{\partial p_k}\frac{\partial H}{\partial q_k}\right)+\frac{\partial f}{\partial t}$

Man definiert also die Poisson-Klammer allgemein als

$\{F,G\}_{\mathbf{ab}}:=\nabla_{\mathbf{a}}F \cdot \nabla_{\mathbf{b}}G-\nabla_{\mathbf{b}}F \cdot \nabla_{\mathbf{a}}G=\sum^s_{k=1}\left(\frac{\partial F}{\partial a_k}\frac{\partial G}{\partial b_k}-\frac{\partial F}{\partial b_k}\frac{\partial G}{\partial a_k}\right)$

Eigenschaften

• Antisymmetrie

$\{f,g\}=-\{g,f\} \Rightarrow \{f,f\}=0$

• Bilinearität

$\,\{c_1 f_1+c_2 f_2,g\}=c_1 \{f_1,g\}+ c_2 \{f_2,g\}$

• Produktregel

$\,\{f,gh\}=h\{f,g\}+g\{f,h\}$

• Jacobi-Identität

$\,\{f,\{g,h\}\}+\{g,\{h,f\}\}+\{h,\{f,g\}\}=0$

• Invarianz

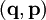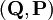Physikalisch liegt es nahe anzunehmen, dass die Zeitentwicklung einer Eigenschaft eines Systems nicht von den verwendeten Koordinaten abhängen sollte. Damit sollten auch die Poisson-Klammern unabhängig von den verwendeten kanonischen Koordinaten sein. Seien $(\mathbf{q},\mathbf{p})$ und $(\mathbf{Q},\mathbf{P})$ zwei verschiedene Sätze von Koordinaten, die durch kanonische Transformationen transformiert werden, so gilt

$\{f,g\}_{\mathbf{qp}}=\{f,g\}_{\mathbf{QP}}=\{f,g\}$.

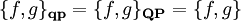Der Beweis für die Invarianzeigenschaft ist länglich, sodass wir ihn hier auslassen.

Fundamentale Poisson-Klammern

Für die kanonische Mechanik wichtig sind die fundamentalen Poisson-Klammern

$\left \{ q_k, p_l \right \} = \delta_{kl}$

$\left \{ q_k, q_l \right \} = 0$

$\left \{ p_k, p_l \right \} = 0$

welche einfach aus den trivialen Beziehungen

$\frac{\partial q_k}{\partial p_l}=0$

$\frac{\partial p_k}{\partial q_l}=0$

$\frac{\partial p_k}{\partial p_l}=\delta_{kl}$

folgen.

Dabei ist δ_kl das Kronecker-Delta.

Anwendung

• Die Poisson-Klammer kann dazu benutzt werden, um die zeitliche Änderung von Observablen durch die Dynamik des Systems zu bestimmen. Es gilt für eine Observable $f(\mathbf{q},\mathbf{p},t)$

$\frac{\mathrm{d} f}{\mathrm{d} t}=\{f,H\} + \frac{\partial f}{\partial t},$

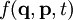
• Insbesondere kann man mit dieser Gleichung Konstanten der Bewegung (Erhaltungsgrößen) charakterisieren. Eine Observable 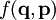$f(\mathbf{q},\mathbf{p})$ ist nämlich genau dann eine Erhaltungsgröße, wenn

$0=\{f,H\} + \frac{\partial f}{\partial t}$

gilt. Ist f nicht explizit zeitabhängig, wird daraus

$\,0=\{f,H\}$

• Dual zur Bewegungsgleichung der Observablen ist die Liouville-Gleichung, die die Dynamik der Verteilungsdichte in der statistischen Mechanik beschreibt:

$\dot{\rho}=\{H,\rho\}.$

• In der Quantenmechanik wird im Rahmen der kanonischen Quantisierung die Poisson-Klammer durch 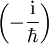$\left(-\frac{{\rm i}}{\hbar}\right)$ mal den Kommutator ersetzt. Die Liouville-Gleichung findet ihre Entsprechung dabei in der Von-Neumann'schen Bewegungsgleichung.

• Sowohl die Phasenraumfunktionen der kanonischen Mechanik als auch die Operatoren der Quantenmechanik bilden mit ihren Klammern jeweils eine Liealgebra.

Siehe auch

• Symplektische Mannigfaltigkeit
• Kanonische Transformation