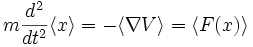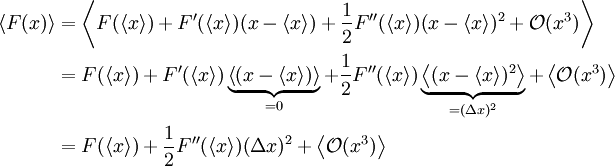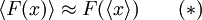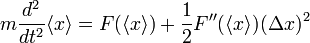- Ehrenfesttheorem
-
Das Ehrenfest-Theorem, benannt nach dem österreichischen Physiker Paul Ehrenfest, stellt innerhalb der Physik einen Zusammenhang zwischen der klassischen Mechanik und der Quantenmechanik her. Es besagt, dass unter bestimmten Bedingungen die klassischen Bewegungsgleichungen für die Mittelwerte der Quantenmechanik gelten; die klassische Mechanik also in gewissem Maße in der Quantenmechanik enthalten ist (Korrespondenzprinzip).
Mathematisch drückt sich das in seiner allgemeinsten Form so aus, dass die vollständige Zeitableitung des Erwartungswertes eines quantenmechanischen Operators mit dem Kommutator dieses Operators und des Hamiltonoperators wie folgt in Zusammenhang stehen:
Dabei stellt O einen quantenmechanischen Operator und
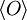 dessen Erwartungswert dar.
dessen Erwartungswert dar.Inhaltsverzeichnis
Klassisches Analogon
Im Hamilton-Formalismus der klassischen Mechanik gilt für die Zeitentwicklung einer Phasenraumfunktion:
mit der Poisson-Klammer
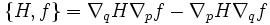 . Bei der Quantisierung wird die Poisson-Klammer durch den mit
. Bei der Quantisierung wird die Poisson-Klammer durch den mit 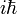 multiplizierten Kommutator ersetzt. Das quantenmechanische Analogon einer Phasenraumfunktion ist ein Operator (Observable). Somit ist das Ehrenfest-Theorem das direkte Analogon zu der obigen klassischen Aussage.
multiplizierten Kommutator ersetzt. Das quantenmechanische Analogon einer Phasenraumfunktion ist ein Operator (Observable). Somit ist das Ehrenfest-Theorem das direkte Analogon zu der obigen klassischen Aussage.Anwendung
Für den Spezialfall des nicht explizit zeitabhängigen Impulsoperators
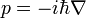 gilt somit:
gilt somit:Da weiterhin für die Zeitentwicklung des Ortsoperators folgt
lässt sich folgern:
Klassische Näherung
Der Erwartungswert der Kraft F(x) lässt sich in eine Taylorreihe um den Erwartungswert von x entwickeln:
Berücksichtigt man nur den ersten Summanden, so erhält man
und somit
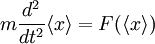 .
.
In Worten bedeutet dies, dass sich der Erwartungswert der Position auf einer klassischen Bahn bewegt, d.h. der klassischen Bewegungsgleichung folgt. Das Ehrenfest-Theorem führt somit direkt auf eine Analogie der Quantenmechanik zur klassischen Mechanik - hier in Form des zweiten Newton'schen Axioms
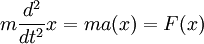 .
.
Die Annahme (*) und damit auch die klassische Bewegungsgleichung für quantenmechanische Erwartungswerte gelten allerdings nur dann exakt, falls die Kraft F(x) eine lineare Funktion der Position x ist. Dies gilt für die einfachen Fälle des harmonischen Oszillators oder des freien Teilchens (dann verschwinden alle Ortsableitungen der Kraft vom Grad größer gleich 2). Außerdem kann man sagen, dass (*) gilt, wenn die Breite der Aufenthaltswahrscheinlichkeit klein ist gegenüber der typischen Längenskala auf der die Kraft F(x) variiert. Die Bewegungsgleichung für Erwartungswerte lautet mit der nächsten nichtverschwindenden Korrektur zur klassischen Bewegungsgleichung:
Herleitung
Es sei das betrachtete System im Quantenzustand Ψ. Man erhält somit für die Zeitableitung des Erwartungswertes eines Operators O:
![\frac{d}{dt}\langle O \rangle = \frac{d}{dt}\int \Psi^* O \Psi dV = \int \left[\left(\frac{\partial \Psi^*}{\partial t}\right)O\Psi + \Psi^*\left(\frac{\partial O}{\partial t}\right)\Psi + \Psi^* O \left(\frac{\partial \Psi}{\partial t}\right)\right]dV](/pictures/dewiki/53/5562da02ee2207313d766f300725a310.png)
![=\int \left[ \left(\frac{\partial \Psi^*}{\partial t}\right) O \Psi + \Psi^* O \left(\frac{\partial \Psi}{\partial t}\right)\right]dV + \left\langle \frac{\partial O}{\partial t}\right\rangle](/pictures/dewiki/98/b3d5f439b1d7f11167c27c37f9b01f88.png)
Man betrachtet nun die Schrödingergleichung
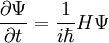
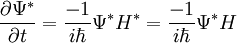
Im zweiten Schritt wurde mit H = H * ausgenutzt, dass der Hamilton-Operator selbstadjungiert ist. Einsetzen dieser Relationen liefert nun:
![\frac{d}{dt}\langle O\rangle = \frac{1}{i\hbar}\int [-\Psi^* HO \Psi + \Psi^* OH\Psi ]dV + \left\langle\frac{\partial O}{\partial t}\right\rangle=\frac{1}{i\hbar}\langle[O,H]\rangle + \left\langle \frac{\partial O}{\partial t}\right\rangle = \frac{i}{\hbar}\langle[H,O]\rangle + \left\langle \frac{\partial O}{\partial t}\right\rangle](/pictures/dewiki/48/08248173702f4b70527d94835c2c4bd6.png)
Siehe auch
Literatur
- Leslie E. Ballentine: Quantum Mechanics: A Modern Development 1. Auflage. World Scientific Publishing, Singapore 1998, ISBN 981-02-4105-4
- P. Ehrenfest: Bemerkung über die angenäherte Gültigkeit der klassischen Mechanik innerhalb der Quantenmechanik Zeitschrift für Physik A Ausgabe 45, Nummern 7-8 / Juli, 1927, Seiten 455-457.
Wikimedia Foundation.

![\frac{d}{dt}\langle O\rangle = \frac{i}{\hbar }\langle [H,O] \rangle + \left\langle \frac{\partial O}{\partial t}\right\rangle](/pictures/dewiki/50/2733bfe4850d0cd787b22dadfb3c0a31.png)
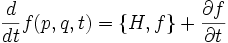
![\frac{d}{dt} \langle p \rangle = \frac{i}{\hbar} \langle [H,p] \rangle = \frac{i}{\hbar} \langle [V,p]\rangle = \frac{i}{\hbar} \langle -\frac{\hbar}{i} \nabla V \rangle = - \langle \nabla V \rangle](/pictures/dewiki/97/a73290ae1b676171399c9a557f40eeef.png)
![\frac{d}{dt}\langle x\rangle = \frac{i}{\hbar}\langle[H,x]\rangle =\frac{1}{m}\langle p\rangle](/pictures/dewiki/56/8a1b2adeca30f43afaa2ef2d1c10a77a.png)