Projection Pursuit

Projection Pursuit (wörtlich Nachverfolgung der Projektion) ist ein statistisches Verfahren, eine Menge hochdimensionaler Daten so zu vereinfachen, dass möglichst "interessante" Strukturen darin aufgedeckt werden. Dazu wird eine Hyperebene (z. B. eine Fläche) in den durch die Daten aufgespannten Raum gelegt, auf welche die Daten projiziert werden.

Der Projection Pursuit wurde zuerst von John W. Tukey und Jerome H. Friedman veröffentlicht^[1] und fand weitere Verbreitung durch die Arbeiten von Peter J. Huber.^[2]

Die Analyse multivariater Daten erfolgt in der Regel durch eine geeignete Abbildung in niedrigere Dimensionen. Bekanntestes Beispiel ist das Streudiagramm, bei dem jeweils zwei Dimensionen die Achsen eines Koordinatensystems bilden. Jede solche Abbildung verdeckt die Sichtbarkeit vorhandener Strukturen stets mehr oder weniger, kann sie aber niemals verstärken.^[3]

Die Idee von Projection Pursuit ist auf die verschiedensten statistischen Probleme angewandt worden:

• Exploratory Projection Pursuit zur Aufdeckung von interessanten Strukturen in Daten
• Projection Pursuit Regression^[4]
• Projection Pursuit Dichteschätzung^[5]
• Projection Pursuit Klassifikation^[6]
• Projection Pursuit Diskriminanzanalyse^[7]

Exploratory Projection Pursuit

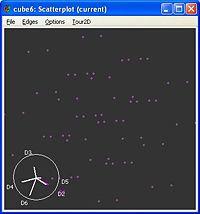Abb. 1: Projektion von Datenpunkten auf den Ecken eines sechsdimensionalen Würfels (cube6) auf eine zweidimensionale Hyperebene. Die Daten sind approximativ standardnormalverteilt in der Ebene.

Abb. 2: Mit dem "Central Mass" Index in GGobi optimierte Lösung des cube6 Datensatzes.

Abb. 3: Visualisierung der "Central Mass" Indexfunktion in GGobi.

Im Exploratory Projection Pursuit wird jeder Hyperebene eine Maßzahl (oder Index) zugeordnet, die angibt wie interessant die enthaltene Struktur ist. In der Arbeit von P. Diaconis und D. Freedman ^[8] wurde gezeigt, dass die meisten Strukturen in den Hyperebenen normalverteilten Daten ähneln (siehe Abb. 1). Viele Maßzahlen messen daher die Distanz der Struktur in der Hyperebene zu einer Normalverteilung.

Danach werden automatisch der Reihe nach alle möglichen Projektionen der Daten auf eine Hyperebene durchgerechnet, die im Vergleich zu den Originaldaten um eine oder mehrere Dimensionen reduziert ist. Werden Datenpunkte als Teil einer interessanten Struktur identifiziert, werden diese aus der Analyse genommen. Das Verfahren wird mit dem reduzierten Datensatz wiederholt, bis keine Struktur mehr erkennbar ist.

Indizes

Die multivariaten Daten werden in der Regel mit $Z = S_X^{-1/2}(X-\bar{x})$ transformiert, so dass die Mittelwerte der Variablen Z gleich Null sind und die Varianz-Kovarianz-Matrix S_Z die Einheitsmatrix ist. Wenn dann α die Projektionsvektoren für die Hyperebene sind, Y = α^TZ die in die Hyperebene projizierten Daten, Φ die Dichtefunktion der Standardnormalverteilung (bzw. der entsprechenden Normalverteilung, wenn Y = α^TX statt Y = α^TZ benutzt wird) und f die Dichtefunktion der projizierten Daten in der Hyperebene, dann wurde unter anderem folgende Indizes, die dann maximiert werden, vorgeschlagen:

Friedman-Tukey-Index^[1]

Der Index $I_{FT}(\alpha) = \int f(y)^2 dy = E(f(y))$ wird minimiert durch eine parabolische Dichtefunktion, welche sehr ähnlich zur Dichtefunktion einer Standardnormalverteilung ist.

Entropy-Index^[2]

$I_{E}(\alpha) = \int f(y)\log(f(y)) dy = E(log(f(y)))$ ist die Entropie, die ebenfalls minimiert wird durch die Standardnormalverteilung.

Legendre-Index^[3], Hermite-Index^[9] und Natural-Hermite-Index^[10]

$I_{L}(\alpha) = \int (f(y)-\Phi(y))^2 \frac{1}{2^{dim(Y)}\Phi(y)} dy$,

$I_{H}(\alpha) = \int (f(y)-\Phi(y))^2 dy$ und

$I_{NH}(\alpha) = \int (f(y)-\Phi(y))^2 \Phi(y) dy$.

Alle drei Indizes messen den Abstand zur Standardnormalverteilung, sie unterscheiden sich nur in der Art der Gewichtung der Differenz zwischen der Dichte der projizierten Daten und der Standardnormalverteilung.

χ²-Index^[11]

partitioniert eine (zweidimensionale) Ebene in 48 Zellen und wendet dann einen χ²-Anpassungstest zum Vergleich der Beobachtungszahl in jeder Zelle mit der Zahl der Beobachtungen unter Annahme der Standardnormalverteilung.

Im Prinzip kann jede Teststatistik, die zu einem Test auf Normalverteilung gehört, als Index benutzt werden. Eine Maximierung führt dann zu den Hyperebenen, in denen die Daten nicht normalverteilt sind. Spezielle Versionen der Indizes I_L, I_H und I_NH werden maximiert durch bestimmten Strukturen, z.B. Zentrales Loch oder Zentrale Masse.

Die unbekannte Dichtefunktion f(y) der projizierten Daten wird entweder mittels eines Kerndichteschätzer oder durch eine orthonormale Funktionsexpansion geschätzt.

Verwandte Methoden

Als Spezialfälle des Exploratory Projection Pursuit kann man

• die Grand Tour betrachten, bei der die Strukturen durch den Betrachter selbst in den Grafiken entdeckt werden, und
• die Hauptkomponentenanalyse, bei der der Index durch I_PCA(α) = Var(α^TX) beschrieben wird.

Projection Pursuit Regression

Im Regressionfall wird die unbekannte Regressionsfunktion $f(x)=\sum_k f_k(\alpha_k^Tx)$ iterativ durch Regressionsfunktionen f_k auf den projizierten Daten dargestellt:

1. $y_i^{(1)}=y_i$ sind die beobachteten Regressionswerte
2. Finde α_k so, dass $\epsilon_k = \sum_i (y_i^{(k)}-f_k(\alpha_k^Tx_i))^2$ minimal ist
3. Setze $y_i^{(k+1)}=y_i^{(k)}-f_k(\alpha_k^Tx_i)$
4. Iteriere Schritte 2-3 solange bis $\epsilon_k$ kleiner als eine vorgebene Schranke ist oder nicht mehr kleiner wird
5. Verbessere die Approximation in dem für jedes α_k nochmal $\sum_i \left(y_i-\sum_{l\neq k} f_l(\alpha_l^Tx_i) - f_k(\alpha_k^Tx_i)\right)^2$ minimiert wird

Projection Pursuit Dichteschätzung

Auch im Fall der Dichteschätzung wird eine iteratives Verfahren benutzt. Die unbekannte Dichtefunktion f(x) wird approximiert als Produkt von Dichtefunktionen der projizierten Daten:

$f(x) = \Phi(x) \prod_k f_k(\alpha_k^Tx)$

mit Φ(x) die Dichtefunktion der multivariaten Normalverteilung mit den Parametern $\bar{x}$ und S geschätzt aus den Daten. Dann wird schrittweise die Normalverteilungsdichte korrigiert. Im Gegensatz zum Regressionsfall ist jedoch der Algorithmus wesentlich komplizierter, da hier keine Beobachtungen y_i zu Verfügung stehen an die angepasst werden kann.

Siehe auch

• Hauptkomponentenanalyse
• Grand Tour (Statistik)
• Clusteranalyse

Weblinks

• Webseite von Jerome H. Friedman
• N-Land: a Graphical Tool for Exploring N-Dimensional Data
• GGobi: freie Software zur statistischen Analyse; bietet Projection Pursuit.
• In R in der Bibliothek stats den Befehl ppr

Einzelnachweise

1. ↑ ^{a b} J. H. Friedman and J. W. Tukey (Sept. 1974): A Projection Pursuit Algorithm for Exploratory Data Analysis. IEEE Transactions on Computers C-23 9: S. 881 ff. doi: 10.1109/T-C.1974.224051. ISSN 0018-9340.
2. ↑ ^{a b} P.J. Huber (1985): Projection pursuit, Annals of Statistics, 13, Nr. 2, S. 435 ff.
3. ↑ ^{a b} J.H. Friedman (1987): Exploratory projection pursuit, Journal of the American Statistical Assoc., 82, Nr. 397, S. 249-266.
4. ↑ J.H. Friedman, W. Stuetzle (1981): Projection pursuit regression, Journal of the American Statistical Association 76, S. 817-823
5. ↑ J.H. Friedman, W. Stuetzle, A. Schröder (1984): Projection pursuit density estimation, Journal of the American Statistical Association 79, S. 599-608
6. ↑ J.H. Friedman, W. Stuetzle (1981): Projection pursuit classification, unpublished manuscript
7. ↑ J. Polzehl (1995): Projection pursuit discriminant analysis, Computational Statistics & Data Analysis 20, S. 141-157
8. ↑ P. Diaconis, D. Freedman (1989): Asymptotics of graphical projection pursuit, The Annals of Statistics 17, Nr. 1, S. 793-815.
9. ↑ P. Hall (1989): On polynomial-based projection indices for exploratory projection pursuit, The Annals of Statistics 17, Nr. 2, S. 589-605.
10. ↑ D. Cook, A. Buja, J. Cabrera (1993): Projection pursuit indices based on orthonormal function expansion, Journal of Computational and Graphical Statistics 2, Nr. 3, S. 225-250
11. ↑ C. Posse (1995): Projection pursuit exploratory data analysis, Computational Statistics and Data Analysis, 20, S. 669-687.