Kerndichteschätzer

Die Kerndichteschätzung (auch Parzen-Fenster-Methode,^[1] englisch: Kernel Density Estimation, KDE) ist ein Verfahren zur Schätzung der Wahrscheinlichkeitsverteilung einer Zufallsvariable.

In der klassischen Statistik geht man davon aus, dass statistische Phänomene einer bestimmten Wahrscheinlichkeitsverteilung folgen und dass sich diese Verteilung in Stichproben realisiert. In der nichtparametrischen Statistik werden Verfahren entwickelt, um aus der Realisation einer Stichprobe die zu Grunde liegende Verteilung zu identifizieren. Ein bekanntes Verfahren ist die Erstellung eines Histogramms. Nachteil dieses Verfahrens ist, dass das resultierende Histogramm nicht stetig ist. Vielfach ist aber davon auszugehen, dass die zu Grunde liegende Verteilung als stetig betrachtet werden kann. So etwa die Verteilung von Wartezeiten in einer Schlange oder die Rendite von Aktien.

Der im folgenden beschriebene Kerndichteschätzer ist dagegen ein Verfahren, das eine stetige Schätzung der unbekannten Verteilung ermöglicht. Genauer: die Kerndichteschätzung ist ein gleichmäßig konsistenter, stetiger Schätzer der Lebesgue-Dichte eines unbekannten Wahrscheinlichkeitsmaßes durch eine Folge von Dichten.

Beispiel

Kerndichteschätzung

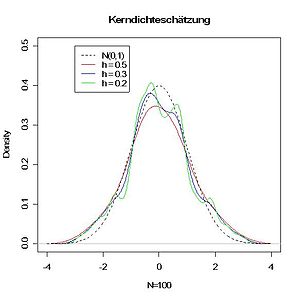
Im folgenden Beispiel wird die Dichte einer Standardnormalverteilung (schwarz gestrichelt) durch Kerndichteschätzung geschätzt. In der konkreten Situation des Schätzens ist diese Kurve natürlich unbekannt und soll durch die Kerndichteschätzung geschätzt werden. Es wurde eine Stichprobe (vom Umfang 100) generiert, die gemäß dieser Standardnormalverteilung verteilt ist. Mit verschiedenen Bandbreiten h wurde dann eine Kerndichteschätzung durchgeführt. Man sieht deutlich, dass die Qualität des Kerndichteschätzers von der gewählten Bandbreite abhängt. Eine zu kleine Bandbreite erscheint "verwackelt", während eine zu große Bandbreite zu "grob" ist.

Kerne

Kerndichteschätzung mit Cauchykern

Mit Kern wird die stetige Lebesgue-Dichte k eines fast beliebig zu wählenden Wahrscheinlichkeitsmaßes K bezeichnet. Mögliche Kerne sind etwa:

• Gaußkern $k(t):=\frac{1}{\sqrt{2\pi}}\exp \left(-\frac{1}{2}t^2\right)$

• Cauchy-Kern $k(t):=\frac{1}{\pi(1+t^2)}$

• Picard-Kern $k(t):=\frac{1}{2}\exp(-|t|)$

• Epanechnikov-Kern $k(t) :=\begin{cases} \frac{3}{4} ( 1- t^2 ), & \text{wenn }t\in [-1;1]\\ 0, & \text{sonst} \end{cases}$

Diese Kerne sind Dichten von ähnlicher Gestalt wie der abgebildete Cauchykern. Der Kerndichteschätzer stellt eine Überlagerung in Form der Summe entsprechend skalierter Kerne dar, die abhängig von der Stichprobenrealisation positioniert werden. Die Skalierung und ein Vorfaktor gewährleisten, dass die resultierende Summe wiederum die Dichte eines Wahrscheinlichkeitsmaßes darstellt. Der folgenden Abbildung wurde eine Stichprobe vom Umfang 10 zu Grunde gelegt, die als schwarze Kreise dargestellt ist. Darüber sind die Cauchykerne (grün gestrichelt) dargestellt, aus deren Überlagerung der Kerndichteschätzer resultiert (rote Kurve).

Der Epanechnikov-Kern ist dabei derjenige Kern, der unter allen Kernen die mittlere quadratische Abweichung des zugehörigen Kerndichteschätzers minimiert.

Der Kerndichteschätzer

Ist $x_1,\ldots,x_n\in\mathbb{R}$ eine Stichprobe, k ein Kern, so wird der Kerndichteschätzer zur Bandbreite h > 0 definiert als: $\tilde f_{n}:\mathbb{R}\to\mathbb{R}_{+}$, $\tilde f_{n}(t)=\frac{1}{n}\sum_{j=1}^{n}k_h(t-x_j)=\frac{1}{nh}\sum_{j=1}^{n}k\left(\frac{t-x_j}{h}\right)$.

Die Wahl der Bandbreite h ist entscheidend für die Qualität der Approximation. Mit entsprechender, in Abhängigkeit vom Stichprobenumfang gewählter Bandbreite konvergiert die Folge $\tilde f_n$ der Kerndichteschätzer fast sicher gleichmäßig gegen die Dichte des unbekannten Wahrscheinlichkeitsmaßes. Diese Aussage wird im folgenden Satz von Nadaraja konkretisiert.

Satz von Nadaraja

Der Satz liefert die Aussage, dass mit entsprechend gewählter Bandbreite eine beliebig gute Schätzung der unbekannten Verteilung durch Wahl einer entsprechend großen Stichprobe möglich ist.

Sei k ein Kern von beschränkter Variation. Die Dichte f eines Wahrscheinlichkeitsmaßes sei gleichmäßig stetig. Mit $0<\alpha<\frac{1}{2}$ und c > 0 seien für $n\in\mathbb{N}$ die Bandbreiten $h(n)=\frac{c}{n^\alpha}$ definiert. Dann konvergiert die Folge der Kerndichteschätzer $\tilde f_{n}$ mit Wahrscheinlichkeit 1 gleichmäßig gegen f, d. h. $P\left(\left\{x\in\mathbb{R}^{\infty}\vert\lim_{n\to\infty}\sup_{t\in\mathbb{R}}\left|\tilde{f}_n(t)-f(t)\right|=0\right\}\right)=1$

Anwendung

Die Kerndichteschätzung wird von Statistikern seit etwa 1950 eingesetzt und wird in der Ökologie häufig zur Beschreibung des Aktionsraumes eines Tieres verwendet, seitdem diese Methode in den 1990ern in den Wissenschaftszweig Einzug hielt. Damit kann die Wahrscheinlichkeit errechnet werden, mit der ein Tier sich in einem bestimmten räumlichen Bereich aufhält. Aktionsraum-Voraussagen werden durch farbige Linien (z. B. Isolinien) dargestellt.^[2]

Siehe auch

Schätzfunktion, Histogramm, Empirische Verteilungsfunktion, Stichprobe, Dichteschätzer

Einzelnachweise

1. ↑ Parzen E. (1962). On estimation of a probability density function and mode, Ann. Math. Stat. 33, pp. 1065-1076.
2. ↑ Arthur R. Rodgers, John G. Kie: HRT: Home Range Tools for ArcGIS®. User’s Manual. 10. August 2011, S. 6ff (ttp://flash.lakeheadu.ca/~arodgers/hre/HRT%20Users%20Manual%20Draft%20August%2010%202011.pdf, abgerufen am 24. Oktober 2011).