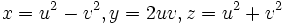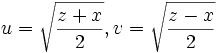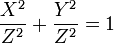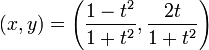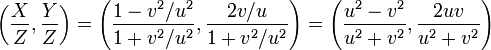Pythagoreisches Zahlentripel

Ein pythagoreisches Tripel oder pythagoreisches Zahlentripel wird von drei natürlichen Zahlen gebildet, die als Längen der Seiten eines rechtwinkeligen Dreiecks vorkommen können.

Sie finden sich bereits auf babylonischen Tontafeln, die in die Zeit der Hammurabi-Dynastie datiert werden (1829 bis 1530 v. Chr). Die Keilschrifttafel Plimpton 322 enthält 15 verschiedene pythagoreische Tripel, u. a. (56,90,106), (119,120,169) sowie (12709,13500,18541), was auf ein Verfahren zur Berechnung solcher Tripel schließen lässt.

Das indische Baudhayana-Sulbasutra aus dem 6. Jahrhundert vor Christus enthält fünf pythagoreische Tripel.^[1]

Pythagoreische Tripel wurden auch von Diophant behandelt. Wegen des pythagoreischen Lehrsatzes sind sie genau die positiven ganzzahligen Lösungen der diophantischen Gleichung

x² + y² = z²

Wenn x,y,z gekürzt sind, d.h., wenn sie keinen gemeinsamen Teiler haben, dann spricht man von einem primitiven pythagoreischen Tripel. Bei jedem primitiven Tripel ist z ungerade, und von den Zahlen x und y ist eine gerade und die andere ungerade.

Beispiele

• Das kleinste pythagoreische Tripel ist (3,4,5). Es ist primitiv. Es wird in der Zwölfknotenschnur zur Herstellung eines rechten Winkels benutzt.
• (5,12,13) ist ein primitives Tripel.
• (15,20,25) und (15,36,39) sind nicht primitiv.

Erzeugung der pythagoreischen Tripel

Die Formeln

$x = u^2-v^2, y = 2uv, z = u^2+v^2 \$

liefern für beliebige 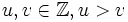$u,v \in \mathbb{Z}, u>v$ ein pythagoreisches Tripel. Sind x,y teilerfremd, so lässt sich jedes primitive pythagoreische (x,y,z) darstellen.

Durch Lösen dieses Gleichungssystems erhält man:

$u = \sqrt{\frac{z+x}{2}}, v = \sqrt{\frac{z-x}{2}}$

Man erhält jedes pythagoreische Tripel, wenn man das bestimmte (primitive) Tripel x,y,z berechnet und mit einer beliebigen natürlichen Zahl n multipliziert: nx,ny,nz.

Beispiele:

• 2,1 liefert das Tripel (3,4,5)
• 3,1 liefert das Tripel (6,8,10), welches nicht primitiv ist, weil 3 und 1 beide ungerade sind und dem mit 2 multiplizierten Tripel von (3,4,5) entspricht.
• 3,2 liefert das Tripel (5,12,13)
• Multiplikation mit 7 liefert (35,84,91)

Herleitung der Formel zur Bildung der Pythagoreischen Tripel

Dividiert man den Satz des Pythagoras X² + Y² = Z² durch Z², so erhält man die Koordinatengleichung eines Einheitskreises:

$\frac{X^2}{Z^2} + \frac{Y^2}{Z^2} = 1$

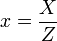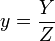Die Zahlen $x=\frac{X}{Z}$ und $y=\frac{Y}{Z}$ sind rational und positiv und erfüllen die Gleichung

x² + y² = 1.

Also sind (x,y) Punkte mit rationalen Koordinaten auf dem Einheitskreis. Die Gerade durch die Punkte (-1,0) und (x,y) schneidet die y-Achse im Punkt (0,t). Man erhält damit den Anstieg

$t = \frac{y}{x+1} = \frac{v}{u}$,

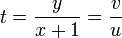wobei t eine rationale Zahl ist und v, u teilerfremde natürliche Zahlen sind.

Setzt man diese Gleichung in die Gleichung des Einheitskreises ein, erhält man:

1 = x² + y² = x² + t²(x + 1)²

0 = (x² − 1) + t²(x + 1)² = (x + 1)[(x − 1) + t²(x + 1)].

Da uns die erste Lösung x=-1 nicht interessiert, betrachten wir nur die zweite:

(x − 1) + t²(x + 1) = 0

$x = \frac{1-t^2}{1+t^2}$

$y = t \cdot (x+1) = t \cdot \left(\frac{1-t^2}{1+t^2}+1 \right)=\frac{2t}{1+t^2}$

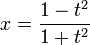
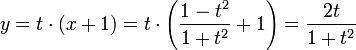
Die Koordinaten (x,y) sind damit:

$(x,y) = \left(\frac{1-t^2}{1+t^2},\frac{2t}{1+t^2} \right)$

oder

$\left(\frac{X}{Z},\frac{Y}{Z}\right) = \left(\frac{1-v^2/u^2}{1+v^2/u^2},\frac{2v/u}{1+v^2/u^2}\right) = \left(\frac{u^2-v^2}{u^2+v^2},\frac{2uv}{u^2+v^2}\right)$

Damit erhält man das pythagoreische Tripel:

(X,Y,Z) = (u² − v²,2uv,u² + v²)

Nun kann es vorkommen, dass u² − v², 2uv und u² + v² doch einen gemeinsamen Teiler D besitzen. Aus u = 3,v = 1 würde beispielsweise

x = 8,y = 6,z = 10 folgen.

Um ein primitives pythagoreisches Tripel zu erhalten, muss man noch durch den gemeinsamen Teiler D dividieren.

$(X,Y,Z) = (\frac{u^2-v^2}{D},\frac{2uv}{D},\frac{u^2+v^2}{D})$.

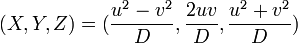Wegen (u² + v²) + (u² − v²) = 2u² und (u² + v²) − (u² − v²) = 2v² sowie der Voraussetzung, dass u und v keinen gemeinsamen Teiler haben, folgt:

D = 2

Die ersten primitiven pythagoreischen Tripel

Nach diesen Regeln erhält man als primitive pythagoreische Tripel zum Beispiel (geordnet nach u+v):

u	v	x	y	z
2	1	3	4	5
4	1	15	8	17
3	2	5	12	13
6	1	35	12	37
5	2	21	20	29
4	3	7	24	25
8	1	63	16	65
7	2	45	28	53
5	4	9	40	41
10	1	99	20	101
9	2	77	36	85
8	3	55	48	73
7	4	33	56	65
6	5	11	60	61

Zwei Folgen von pythagoreischen Tripeln sind noch bemerkenswert:

• für v = 1 (und gerades u):
  (3, 4, 5), (15, 8, 17), (35, 12, 37), (63, 16, 65), (99, 20, 101), (143, 24, 145),…, (4n²-1, 4n, 4n²+1),…
  also für jede natürliche Zahl n ein Tripel, das die Zahl 4n enthält, und bei dem sich die beiden anderen Zahlen um genau 2 unterscheiden.
• für v = u-1:
  (3, 4, 5), (5, 12, 13), (7, 24, 25), (9, 40, 41), (11, 60, 61), (13, 84, 85),…, (2n+1, 2n²+2n, 2n²+2n+1),…
  also für jede ungerade 2n+1 (außer 1) ein Tripel, bei dem die Zahl 2n+1 die kleinste Zahl ist und sich die beiden anderen Zahlen um genau 1 unterscheiden.

Zusammenhang mit den heronischen Dreiecken

Jedes zu einem pythagoreischen Tripel gehörige Dreieck ist ein heronisches Dreieck. Jedes heronische Dreieck lässt sich in zwei rechtwinklige Dreiecke zerlegen, die durch pythagoreische Tripel aus rationalen Zahlen gegeben sind.

Die Fermatsche Gleichung

Eine Verallgemeinerung der pythagoreischen Tripel erhält man, wenn man den Exponenten 2 durch eine natürliche Zahl n ersetzt. Man untersucht also die diophantische Gleichung

$x^n + y^n = z^n \qquad ( 2 < n \in \mathbb{N} )$

und sucht nach Lösungen durch natürliche (oder ganze) Zahlen x,y,z unter Ausschluss der trivialen Lösungen, bei denen eine der drei Zahlen gleich Null ist.

Pierre de Fermat stellte um das Jahr 1637 die Behauptung auf, dass es keine derartigen Tripel gibt. Obwohl er keinen Beweis angab, wird diese Vermutung als großer Fermatscher Satz bezeichnet. Jahrhundertelang konnte kein Beweis gefunden werden. Die Suche danach führte aber zu vielen interessanten Ergebnissen, insbesondere in der Zahlentheorie. 1995 konnte der Mathematiker Andrew Wiles den Satz von Fermat schließlich beweisen.

Weblinks

• Vertiefendes zur den Pythagoreischen Zahlentripeln und Beweise
• Pythagoreische Tripel

Einzelnachweise

1. ↑ Helmuth Gericke: Mathematik in Antike, Orient und Abendland. Marix Verlag, Wiesbaden 2005, ISBN 3-937715-71-1, S. 68