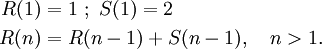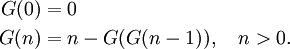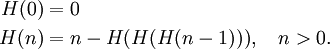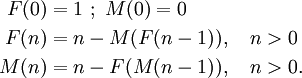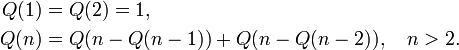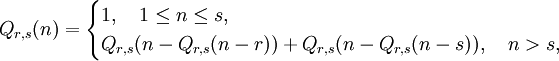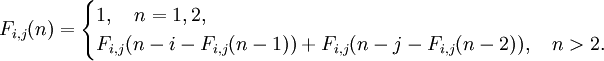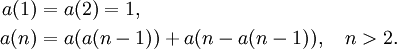- Q-Folge
-
In der Mathematik sind die Hofstadter-Folgen Angehörige einer Familie ganzzahliger Folgen, die durch nichtlineare Differenzengleichungen beschrieben werden.
Inhaltsverzeichnis
Hofstadter-Folgen aus dem Buch Gödel, Escher, Bach: ein Endloses Geflochtenes Band
Die ersten Hofstadter-Folgen wurden von Douglas Robert Hofstadter in seinem Buch Gödel, Escher, Bach beschrieben. In der Reihenfolge ihrer Einführung in Kapitel III: Figur und Hintergrund (Figur-Figur-Folge) und Kapitel V: Rekursive Strukturen und Prozesse (restliche Folgen):
Hofstadters Figur-Figur-Folgen
Hofstadters Figur-Figur- (auch: R-und-S-) Folgen sind wie folgt beschrieben: [1][2]
Die Folge {S(n)} wird dabei beschrieben als Folge der positiven ganzen Zahlen, die nicht in der Folge {R(n)} enthalten sind. Die ersten Zahlen dieser Folgen sind:
- R: 1, 3, 7, 12, 18, 26, 35, 45, 56, 69, 83, 98, 114, 131, 150, 170, 191, 213, 236, 260, ... (Folge A005228 in OEIS)
- S: 2, 4, 5, 6, 8, 9, 10, 11, 13, 14, 15, 16, 17, 19, 20, 21, 22, 23, 24, 25, ... (Folge A030124 in OEIS)
Hofstadters G-Folge
Hofstadters G-Folge ist wie folgt beschrieben:[3][4]
Die ersten Zahlen dieser Folge sind:
Hofstadters H-Folge
Hoftstadters H-Folge ist wie folgt beschrieben:[5][6]
Die ersten Zahlen dieser Folge sind:
Hofstadters "verheiratete" Folgen
Hofstadters "verheiratete" Folgen sind wie folgt beschrieben:[7][8]
Diese Folgen werden in englischer Sprache entsprechend der us-amerikanischen Originalausgabe von Hofstadters Buch als Female (F) and Male (M) sequences (weibliche und männliche Folgen) bezeichnet; die Bezeichnung als verheiratete Folgen kommt im englischen Originaltext nicht vor und ist ein Übersetzungskompromiss.[9] Gleichwohl kann von Hofstadters Einverständnis mit dieser Namensübertragung ausgegangen werden, da der Autor Deutsch spricht und die deutsche Ausgabe durchgesehen hat.[10]
Die ersten Zahlen dieser Folgen sind:
- F: 1, 1, 2, 2, 3, 3, 4, 5, 5, 6, 6, 7, 8, 8, 9, 9, 10, 11, 11, 12, 13, ... (Folge A005378 in OEIS)
- M: 0, 0, 1, 2, 2, 3, 4, 4, 5, 6, 6, 7, 7, 8, 9, 9, 10, 11, 11, 12, 12, ... (Folge A005379 in OEIS)
Hofstadters Q-Folge
Hofstadters Q-Folge ist wie folgt beschrieben:[11][12]
Die ersten Zahlen dieser Folge sind:
Hofstadter nennt die Elemente dieser Folge "Q-Zahlen"[13]; die Q-Zahl von 6 ist also 4. Die Darstellung der Q-Folge in Hofstadters Buch ist die erste bekannte Erwähnung einer Meta-Fibonacci-Folge in der Literatur.[14]
Während die Elemente der Fibonacci-Folge durch das Summieren der beiden jeweils vorhergehenden Elemente bestimmt werden, bestimmen die beiden jeweils vorhergehenden Elemente einer Q-Zahl, wie weit in der Q-Folge zurückgegangen werden soll, um zu den beiden Summanden zu gelangen. Daher hängen die Indice dieser beiden Summanden von der Q-Folge selbst ab.
Q(1), das erste Element der Folge (die erste Q-Zahl), ist im Verlauf der Berechnung von Elementen der Q-Folge niemals als Summand an der Berechnung weiterer Elemente der Folge beteiligt; es wird allein verwendet, um den Index zu berechnen, mit dem auf das zweite Element der Folge Bezug genommen wird.[15]
Obwohl sich die Elemente der Q-Folge chaotisch zu entwickeln scheinen,[16][17][18][19] können ihre Elemente wie diejenige vieler Meta-Fibonacci-Folgen in aufeinanderfolgende Blöcke gruppiert werden, die die Literatur als Generationen bezeichnet.[20][21] Im Fall der Q-Folge hat die k-te Generation 2k Angehörige.[22] Wenn außerdem g die Generation angibt, der eine Q-Zahl angehört, dann sind die Summanden dieser Q-Zahl, die als Eltern bezeichnet werden, bei weitem am häufigsten in der Generation (g-1) angesiedelt und nur einige wenige in der Generation (g-2), niemals jedoch in einer noch früheren Generation.[23]
Die meisten dieser Feststellungen sind empirische Beobachtungen, da praktisch keine der Eigenschaften der Q-Folge im strengen Sinn bewiesen sind.[24][25][26]
Es ist insbesondere unbekannt, ob die Folge für alle n wohldefiniert ist, das heißt, ob die Folge irgendwo abbricht, weil ihre Produktionsregel versucht, sich auf Elemente zu beziehen, die sich konzeptuell links vom ersten Element Q(1) befinden müssten.[27][28][29]
Verallgemeinerungen der Q-Folge
Die Hofstadter-Huber-Qr,s(n)-Familie
20 Jahre nachdem Hofstadter die Q-Folge zum ersten Mal beschrieben hatte, verwendeten er und Greg Huber den Buchstaben Q, um eine Verallgemeinerung der Q-Folge zu einer Familie von Folgen zu bezeichnen. Die ursprüngliche Q-Folge aus seinem Buch benannten sie in U-Folge um.[30]
Die ursprüngliche Q-Folge wird verallgemeinert, indem (n-1) und (n-2) jeweils durch (n-r) und (n-s) ersetzt werden.[31]
Dies führt zu der Folgenfamilie
wobei s≥2 und r<s ist.
Mit (r,s) = (1,2) ist die ursprüngliche Q-Folge eine Angehörige dieser Familie. Bisher sind nur drei Folgen der Familie Qr,s bekannt, nämlich die U-Folge[32] mit (r,s) = (1,2) (die die ursprüngliche Q-Folge darstellt), die V-Folge[33] mit (r,s) = (1,4) und die W-Folge[34] mit (r,s) = (2,4). Nur für die V-Folge, die sich nicht so chaotisch wie die anderen verhält, ist bewiesen, dass sie nicht abbricht.[35] Ähnlich der ursprünglichen Q-Folge wurden bis heute praktisch keine Eigenschaften der W-Folge im strengen Sinn bewiesen.[36]
Die ersten Zahlen der V-Folge sind:
Die ersten Zahlen der W-Folge sind:
Für andere Werte von (r,s) brechen die Folgen früher oder später ab, d.h. es existiert ein n für das Qr,s(n) nicht definiert ist, weil n-Qr,s(n-r) < 1.[37]
Die Pinn-Fi,j(n)-Familie
1998 schlug Klaus Pinn, Wissenschaftler an der Universität von Münster und in engem Kontakt mit Hofstadter, eine andere Verallgemeinerung von Hofstadters Q-Folge vor, die Pinn F-Folgen nannte.[38]
Die Pinn-Fi,j-Familie ist wie folgt beschrieben:
Pinn führte also die zusätzlichen Konstanten i und j ein, die den Index der Summanden konzeptuell nach links verschiebt (also näher an den Folgenanfang).[39]
Nur die F-Folgen mit (i,j) = (0,0), (0,1), (1,0) und (1,1), deren erste die ursprüngliche Q-Folge darstellt, erscheinen wohldefiniert.[40] Anders als Q(1) sind die ersten Elemente der Pinn-Fi,j(n)-Folgen Summanden bei der Berechnung weiterer Folgenelemente, wenn eine der zusätzlichen Konstanten 1 ist.
Die ersten Zahlen von Pinns F0,1-Folge sind:
Hofstadter-Conway-10.000-Dollar-Folge
Die Hofstadter-Conway-10.000-Dollar-Folge ist wie folgt beschrieben:[41]
Die ersten Zahlen dieser Folge sind:
Diese Folge erhielt ihren Namen durch einen von John Horton Conway ausgelobten Preis in Höhe von 10.000 Dollar für denjenigen, der bestimmte Merkmale ihres asymptotischen Verhaltens zeigen konnte. Das zwischenzeitlich auf 1.000 Dollar reduzierte Preisgeld wurde Collin Mallows zuerkannt.[42] Hofstadter äußerte später, er habe die Folge und ihre Struktur ungefähr 10-15 Jahre vor der Auslobung des Conway-Preises gefunden.[43]
Einzelnachweise
- ↑ Hofstadter (1988) Seite 79
- ↑ Mathworld: Hofstadter Figure-Figure Sequence
- ↑ Hofstadter (1988) Seite 148
- ↑ Mathworld: Hofstadter G-Sequence
- ↑ Hofstadter (1988) Seite 148
- ↑ Mathworld: Hofstadter H-Sequence
- ↑ Hofstadter (1988) Seite 148
- ↑ Mathworld: Hofstadter Male-Female Sequences
- ↑ Hofstadter (1980) Seite 137
- ↑ Hofstadter (1988) Seite 820
- ↑ Hofstadter (1988) Seite 149
- ↑ Mathworld: Hofstadter's Q-Sequence
- ↑ Hofstadter (1988) Seite 149
- ↑ Emerson (2006) Seiten 1, 7
- ↑ Pinn (1999) Seiten 5-6
- ↑ Hofstadter (1988) Seite 149
- ↑ Pinn (1999) Seite 3
- ↑ Pinn (2000) Seite 1
- ↑ Emerson (2006) Seite 7
- ↑ Pinn (1999) Seiten 3-4
- ↑ Balamohan et al. (2007) Seite 19
- ↑ Pinn (1999) Übersicht, Seite 8
- ↑ Pinn (1999) Seiten 4-5
- ↑ Pinn (1999) Seite 2
- ↑ Pinn (2000) Seite 3
- ↑ Balamohan et al. (2007) Seite 2
- ↑ Pinn (1999) Seite 2
- ↑ Emerson (2006) Seite 7
- ↑ Balamohan et al. (2007) Seite 2
- ↑ Balamohan et al. (2007) Seite 2
- ↑ Balamohan et al. (2007) Seite 2
- ↑ Balamohan et al. (2007) Seite 2
- ↑ Balamohan et al. (2007) ganzer Artikel
- ↑ Balamohan et al. (2007) Seite 2
- ↑ Balamohan et al. (2007) Seite 2
- ↑ Balamohan et al. (2007) Seite 2
- ↑ Balamohan et al. (2007) Seite 2
- ↑ Pinn (2000) Seite 16
- ↑ Pinn (2000) Seite 16
- ↑ Pinn (2000) Seite 16
- ↑ Mathworld: Hofstadter-Conway $10,000 Sequence
- ↑ Easy as 1 1 2 2 3; Michael Tempel
- ↑ Pinn (1999) Seite 3
Literatur
- B. Balamohan, A. Kuznetsov, Stephan M. Tanny: On the Behaviour of a Variant of Hofstadter's Q-Sequence. In: Journal of Integer Sequences. 10, Nr. 7, University of Waterloo, Waterloo, Ontario (Canada) 27. Juni 2007, ISSN 1530-7638 (http://www.cs.uwaterloo.ca/journals/JIS/VOL10/Tanny/tanny3.pdf).
- Nathanial D. Emerson: A Family of Meta-Fibonacci Sequences Defined by Variable-Order Recursions. In: Journal of Integer Sequences. 9, Nr. 1, University of Waterloo, Waterloo, Ontario (Canada) 17. März 2006, ISSN 1530-7638 (http://www.cs.uwaterloo.ca/journals/JIS/VOL9/Emerson/emerson6.pdf).
- Douglas Robert Hofstadter: Gödel, Escher, Bach: an Eternal Golden Braid. Vintage Books, New York, New York (USA) 1980, ISBN 0465026567.
- Douglas Robert Hofstadter: Gödel, Escher, Bach: ein Endloses Geflochtenes Band. 11. Auflage. Klett-Cotta, Stuttgart 1988, ISBN 3-608-93037-X.
- Klaus Pinn: Order and Chaos in Hofstadter's Q(n) Sequence. In: Complexity. 4, 1999, S. 41-46 (arXiv:chao-dyn/9803012v2) (http://arxiv.org/abs/chao-dyn/9803012v2).
- Klaus Pinn: A Chaotic Cousin of Conway's Recursive Sequence. In: Experiment. Math.. 9, Nr. 1, 2000, S. 55-66 (arXiv:cond-mat/9808031) (http://arxiv.org/abs/cond-mat/9808031).
- S. Plouffe, N. J. A. Sloane: The Encyclopedia of Integer Sequences. Academic Press, San Diego 1995, ISBN 0125586302.
- N. J. A. Sloane: On-Line Encyclopedia of Integer Sequences.
Wikimedia Foundation.