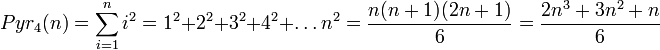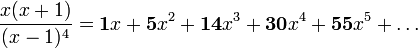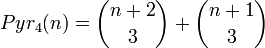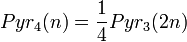Quadratische Pyramidenzahl

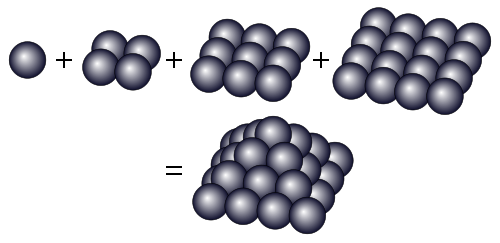
Die Quadratischen Pyramidalzahlen gehören zu den figuierten Zahlen, genauer zu den Pyramidalzahlen. Sie beziffern die Anzahlen von Kugeln, mit denen man eine Pyramide quadratischer Grundfläche bauen kann. Wie die folgende Abbildung es am Beispiel der vierten quadratischen Pyramidalzahl 30 zeigt, sind sie die Summen der ersten Quadratzahlen.

Im Folgenden bezeichne Pyr₄(n) die n-te quadratische Pyramidalzahl.

Es gilt:

$Pyr_4(n)=\sum_{i=1}^n i^2 = 1^2+2^2+3^2+4^2+\ldots n^2 = \frac{n(n+1)(2n+1)}6 = \frac{2n^3 + 3n^2 + n}6$

Die ersten quadratischen Pyramidalzahlen sind

0, 1, 5, 14, 30, 55, 91, 140, 204, 285, 385, … (Folge A000330 in OEIS)

Bei einige Autoren ist die Null keine quadratische Pyramidalzahl, sodass die Zahlenfolge erst mit der Eins beginnt.

Erzeugende Funktion

Die Erzeugende Funktion der quadratischen Pyramidalzahlen lautet:

$\frac{x(x+1)}{(x-1)^4}=\mathbf 1x+\mathbf5 x^2+\mathbf{14}x^3+\mathbf{30}x^4+\mathbf{55}x^5+\ldots$

Beziehungen zu anderen figurierten Zahlen, weitere Darstellungen

Es gilt

$Pyr_4(n)=\binom{n+2}3+\binom{n+1}3$

mit den Binomialkoeffizienten und

$Pyr_4(n)=\frac14 Pyr_3(2n)$

mit den Tetraederzahlen Pyr₃(n).

Außerdem gilt mit Δ_n, der n-ten Dreieckszahl:

Pyr₄(n) = Δ_n + 2T_{n − 1}

Verwandte figurierte Zahlen

• Die anderen Pyramidalzahlen, z.B. die Tetraederzahlen.
• Die Summe zweier aufeinanderfolgender quadratischen Pyramidalzahlen ist eine Oktaederzahl.

Sonstiges

Mit Ausnahme der 1 gibt es nur eine weitere Zahl, die sowohl eine Quadratzahl, als auch eine quadratische Pyramidalzahl ist: 4900 ist die 70, Quadratzahl und die 24. quadratische Pyramidalzahl. Dies wurde von G. N. Watson 1918 bewiesen.

Siehe auch

Faulhabersche Formel

Weblinks

• Eric W. Weisstein: Square Pyramidal Number auf MathWorld (englisch)