- Quadratische Variation
-
In der Mathematik, vor allem der Variationsrechnung und der Theorie der stochastischen Prozesse, ist die Variation (auch totale Variation genannt) einer Funktion ein Maß für das lokale Schwingungsverhalten der Funktion. Besonders bei den stochastischen Prozessen ist die Variation von besonderer Bedeutung, da sie die Klasse der zeitstetigen Prozesse in zwei fundamental verschiedene Unterklassen unterteilt: jene mit endlicher und solche mit unendlicher Variation.
Inhaltsverzeichnis
Definition
Sei
![f:[a,b] \to \R](/pictures/dewiki/98/bb171989e37ee8a1cbb07312813b8ccd.png) eine Funktion auf dem reellen Intervall [a,b]. Das Funktional
eine Funktion auf dem reellen Intervall [a,b]. Das Funktional ![|\cdot |_{[a,b]}](/pictures/dewiki/97/a6f1fa866d93d63dbb64174c88dbc1c0.png) der Variation ist definiert als
der Variation ist definiert als![|f|_{[a,b]} := \sup\left\{ \sum_{k=0}^{n-1} \left|f\!\left(t_{k+1}^{(n)}\right)-f\!\left(t_{k}^{(n)}\right)\right|: n\in\mathbb{N}, a\le t_0^{(n)} < t_1^{(n)} \dots < t_n^{(n)}\le b\right\}](/pictures/dewiki/55/773740cb6a8b3121bcaaaa2c1a0462dc.png) ,
,
also durch die kleinste obere Schranke (Supremum), die alle Summen majorisiert, die sich durch eine beliebig feine Unterteilungen
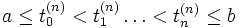 des Intervalls [a,b] ergeben. (Falls sich keine reelle Zahl finden lässt, die alle Summen majorsiert, so wird das Supremum zu plus unendlich gesetzt.)
des Intervalls [a,b] ergeben. (Falls sich keine reelle Zahl finden lässt, die alle Summen majorsiert, so wird das Supremum zu plus unendlich gesetzt.)Für stückweise monotone Funktionen gilt allerdings der folgende Satz:
Ist
![f: [a,b] \to \R](/pictures/dewiki/98/bb171989e37ee8a1cbb07312813b8ccd.png) in den Intervallen
in den Intervallen ![a=[t_0,t_1[,\;,[t_1.t_2[,\ldots [t_{n-1},t_n=b]](/pictures/dewiki/51/3ec9eb232dda2cf57fa2983bdfd133fb.png) jeweils monoton steigend oder fallend, so gilt für die Variation von f die Gleichung
jeweils monoton steigend oder fallend, so gilt für die Variation von f die Gleichung![|f|_{[a,b]}= \sum_{k=0}^{n-1} |f(t_{k+1})-f(t_{k})|](/pictures/dewiki/102/f6d8eb7bec4b329d5fc631802d483ac7.png) .
.
Obige Definition der Variation lässt sich auf Funktionen übertragen, die auf unbeschränkten Intervallen definiert sind und Werte in den komplexen Zahlen oder in normierten Vektorräumen annehmen.
Beispiel einer stetigen Funktion mit unendlicher Variation
Wir wollen zeigen, dass für die auf dem Einheitsintervall [0,1] stetige Funktion
![|f|_{[0,1]}=\infty](/pictures/dewiki/53/5cb76b6aea07b70c7e9855a8a85f7031.png) gilt. Für jedes
gilt. Für jedes  seien
seienDann ist (Zeichnung anfertigen!)
was wegen der Divergenz der harmonischen Reihe für
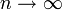 gegen unendlich strebt.
gegen unendlich strebt.Anwendung in der Variationsrechnung
In der Variationsrechnung begegnet man häufig Optimierungsproblemen der folgenden Art:
![\min_{f \in \mathcal{C}} |f|_{[a,b]}](/pictures/dewiki/98/b1723636a22cb3c2e28b6f43899bc0b9.png) ,
,
wobei
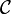 eine vorgegebene Menge von Funktionen ist, etwa alle zweimal stetig differenzierbaren Funktionen mit zusätzlichen Eigenschaften wie
eine vorgegebene Menge von Funktionen ist, etwa alle zweimal stetig differenzierbaren Funktionen mit zusätzlichen Eigenschaften wie 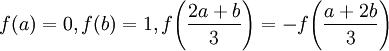 . Ähnliche Probleme führen beispielsweise zur Definition der Splines.
. Ähnliche Probleme führen beispielsweise zur Definition der Splines.Ein weiterer Grund für die Verbreitung der Variation in Optimierungsproblemen ist die folgende Feststellung: Beschreibt die Funktion f den Verlauf eines Objekts in einem eindimensionalen Raum im Laufe der Zeit, dann gibt | f | [a,b] gerade die im Zeitraum [a,b] zurückgelegte Strecke an.
Anwendung in der Stochastik
In der Theorie der stochastischen Prozesse spielt der Begriff der Variation eine besondere Rolle: Eine wichtige Charakterisierung von Prozessen (neben der Einteilung in Klassen wie Markov-, Lévy- oder Gauß-Prozesse) besteht in ihrer Eigenschaft, über endlichen Intervallen fast sicher endliche oder unendliche Variation aufzuweisen:
- Beispiel für einen Prozess fast sicher endlicher Variation: für einen Poisson-Prozess
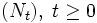 mit Intensität λ gilt wegen der Monotonie
mit Intensität λ gilt wegen der Monotonie ![|N|_{[0,t]} \sim Poi(\lambda t)](/pictures/dewiki/51/3713b9f2a84e7ef5534be81f186ffdcd.png) ;
; - Beispiel für einen Prozess fast sicher unendlicher Variation: der Wiener-Prozess hingegen hat fast sicher unendliche Variation auf jedem Intervall
![[0,t],\;t> 0](/pictures/dewiki/99/c88c2bada84531dab65b71dca44fd15d.png) .
.
Für die Anwendung des Wiener-Prozesses in der Physik zur Erklärung der Brownschen Molekularbewegung hat diese Eigenschaft fatale Folgen: Ein Partikel, dessen Bewegung einem Wiener-Prozess folgt, würde in jedem Teilraum eine unendliche Strecke zurücklegen - im krassen Widerspruch zu den Gesetzen der Physik (das Teilchen hätte unendliche Durchschnittsgeschwindigkeit).
Quadratische Variation
Eine weitere interessante Eigenschaft des Wiener-Prozesses hängt ebenfalls mit dessen Variation zusammen: Ersetzt man in der obigen Definition
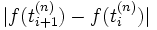 durch
durch 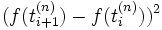 ,
,
so gelangt man zum Begriff der quadratischen Variation
eines stochastischen Prozesses X auf dem Intervall [0,t].
Ein wichtiges Resultat, das sich beispielsweise im Lemma von Itō niederschlägt, ist das folgende: Ist W ein (Standard-)Wiener-Prozess, so gilt für dessen quadratische Variation fast sicher
![\!\,[W,W]_t = t](/pictures/dewiki/54/6352e16092ae8d90cbae848b1bae34f4.png) .
.
Literatur
- Philip Protter: Stochastic Integration and Differential Equations. 2. Auflage. Springer, Berlin 2003, ISBN 978-3-540-00313-7.
Wikimedia Foundation.

![f(t)=\begin{cases} 0&\mbox{falls }t=0,\\ t\cos\frac\pi{2t}&\mbox{falls }t\in(0,1],\end{cases}](/pictures/dewiki/50/2cf5357379b620258d0e95cd94dfa101.png)
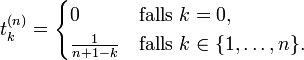
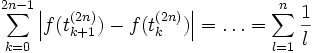
![[X,X]_t,\;t \ge 0](/pictures/dewiki/50/236eb5399d4ca3bae0c5c08f89f58f07.png)