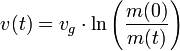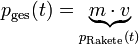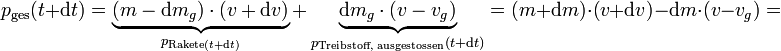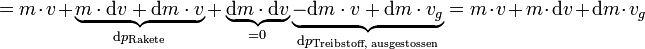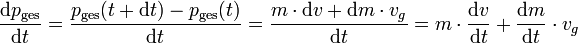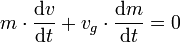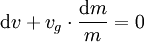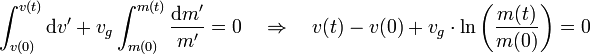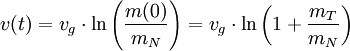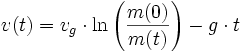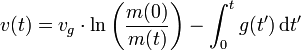- Raketengleichung
-
Die Raketengrundgleichung wurde erstmals 1903 von Konstantin Ziolkowski und unabhängig von ihm später auch von Hermann Oberth und Robert Goddard aufgestellt. Sie beschreibt die grundlegenden Gesetzmäßigkeiten des Raketenantriebs.
Inhaltsverzeichnis
Gleichung
Betrachtet wird der Fall, dass eine einstufige Rakete im gravitationsfreien Vakuum beschleunige. Eine Abbremsung durch Gravitation und Reibung wird nicht in Betracht gezogen. Außerdem wird von Geschwindigkeiten ausgegangen, die weit unterhalb der Lichtgeschwindigkeit liegen, was aber für heutige Raketen erfüllt ist. Die Rakete habe beim Start die Geschwindigkeit Null und stoße Treibstoff mit einer konstanten Ausströmgeschwindigkeit aus. Dann beträgt die Geschwindigkeit nach der Zeit
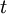 :
:Dabei ist
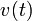 die Raketengeschwindigkeit zur Zeit
die Raketengeschwindigkeit zur Zeit 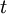 ,
,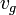 die Ausströmgeschwindigkeit des Antriebsstrahles (typisch: 4 200–4 600 m/s bei aktuellen Flüssigkeitstriebwerken)
die Ausströmgeschwindigkeit des Antriebsstrahles (typisch: 4 200–4 600 m/s bei aktuellen Flüssigkeitstriebwerken)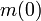 die Startmasse der Rakete und
die Startmasse der Rakete und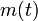 die Masse der Rakete zur Zeit
die Masse der Rakete zur Zeit 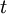 (also die um den verbrauchten Treibstoff verkleinerte Startmasse)
(also die um den verbrauchten Treibstoff verkleinerte Startmasse)
Herleitung
Die Treibstoffgase strömen mit einer (konstanten) Geschwindigkeit
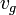 nach hinten aus und beschleunigen die Rakete, die eine Masse
nach hinten aus und beschleunigen die Rakete, die eine Masse 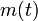 zum Zeitpunkt
zum Zeitpunkt 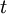 hat, nach vorne.
hat, nach vorne.Der Ausdruck
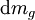 ist die Menge Gas, die in einem Zeitintervall
ist die Menge Gas, die in einem Zeitintervall 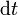 ausgestoßen wird. Hat die Rakete zur Zeit
ausgestoßen wird. Hat die Rakete zur Zeit 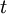 die Masse
die Masse 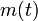 so beträgt zur Zeit
so beträgt zur Zeit 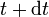 die Masse
die Masse 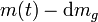 . Die Änderung des Impulses (
. Die Änderung des Impulses (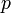 ) der Rakete wird durch den Ausstoß der Masse
) der Rakete wird durch den Ausstoß der Masse 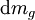 mit der Geschwindigkeit
mit der Geschwindigkeit 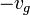 relativ zur Rakete bewirkt (die Ausstoßgeschwindigkeit im Bezugssystem Erde beträgt
relativ zur Rakete bewirkt (die Ausstoßgeschwindigkeit im Bezugssystem Erde beträgt 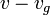 ). Diese Impulsänderung ist eine Kraft, die auf
). Diese Impulsänderung ist eine Kraft, die auf 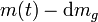 beschleunigend wirkt, nicht auf
beschleunigend wirkt, nicht auf 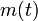 . Die Zunahme der ausgestoßenen Gasmasse entspricht genau der Abnahme der Raketenmasse
. Die Zunahme der ausgestoßenen Gasmasse entspricht genau der Abnahme der Raketenmasse 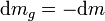 , also ist
, also ist 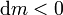 .
.Im Folgenden wird der Impuls des Gesamtsystems bestehend aus Rakete und ausgestoßenem Treibstoff zu verschiedenen Zeiten betrachtet (man beachte, dass die Restmasse der Rakete
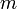 und die Geschwindigkeit der Rakete
und die Geschwindigkeit der Rakete 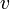 zeitabhängig sind und da im Bezugssystem der Erde gerechnet wird, dass die Ausströmgeschwindigkeit
zeitabhängig sind und da im Bezugssystem der Erde gerechnet wird, dass die Ausströmgeschwindigkeit 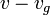 beträgt):
beträgt):Die zeitliche Änderung des Gesamtimpulses berechnet sich aus:
Bei Abwesenheit äußerer Kräfte, wie Gravitations- oder Reibungskräften, ist der Impuls des Gesamtsystems konstant:
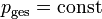 , das heißt
, das heißt 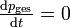 . Man erhält folgende Differentialgleichung:
. Man erhält folgende Differentialgleichung:Teilen durch
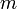 und Multiplizieren mit
und Multiplizieren mit 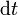 liefert
liefertDie Gleichung wird nun integriert von
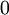 bis
bis 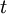 .
.Man erhält die Geschwindigkeit zum Zeitpunkt
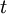 , wobei
, wobei 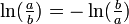 benutzt wird. Schreibt man die Gleichung vektoriell, muss beachtet werden, dass die Ausstoßgeschwindigkeit
benutzt wird. Schreibt man die Gleichung vektoriell, muss beachtet werden, dass die Ausstoßgeschwindigkeit 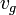 entgegen der Flugrichtung positiv definiert wurde:
entgegen der Flugrichtung positiv definiert wurde: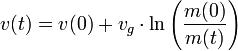 beziehungsweise
beziehungsweise 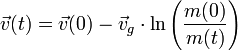
Da zum Startzeitpunkt
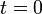 die Rakete noch ruht, ist
die Rakete noch ruht, ist 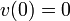 . Als Ergebnis erhält man die Raketengrundgleichung:
. Als Ergebnis erhält man die Raketengrundgleichung:Kontinuierlicher Treibstoffausstoß
Wenn man einen kontinuierlichen Treibstoffausstoß annimmt, sieht die zeitlich abhängige Raketenmasse wie folgt aus:
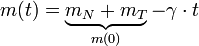 , kontinuierlicher Treibstoffausstoß:
, kontinuierlicher Treibstoffausstoß: 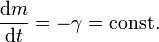
mit
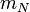 : Masse Nutzlast + Leermasse Rakete,
: Masse Nutzlast + Leermasse Rakete, 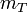 : Treibstoffmasse am Start.
: Treibstoffmasse am Start.Für Zeiten
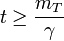 ist der gesamte Treibstoff verbraucht und die maximale Geschwindigkeit erreicht:
ist der gesamte Treibstoff verbraucht und die maximale Geschwindigkeit erreicht:Konsequenz
Als Konsequenz der Gleichung folgt, dass es günstiger ist, Raketen in mehrere Stufen zu unterteilen. Für diese wird die Raketengleichung einzeln gerechnet.
Beispiel
Es sei eine zweistufige Rakete angenommen, deren Brennstufen jeweils zu 90 % der Masse aus Treibstoff bestehen:
Stufe Einzelmasse Leermasse Gesamtmasse Ausströmgeschwindigkeit Nutzlast 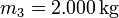
2. Stufe 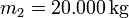
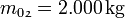
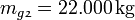
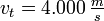
1. Stufe 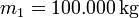
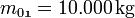
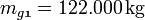
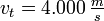
Größe Berechnung Ergebnis Masse bei Brennschluss der ersten Stufe 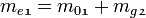
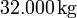
Geschwindigkeit, Brennschluß erste Stufe 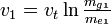
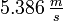
Masse bei Brennschluß der zweiten Stufe 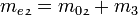
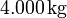
Geschwindigkeit, Brennschluß zweite Stufe 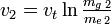
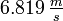
Endgeschwindigkeit 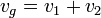
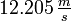
Zum Vergleich sei eine „als Summe der Bestandteile“ angenomme Rakete angenommen:
Praxisbezug
Die Raketengrundgleichung gilt auch im Vakuum des Weltraums (dort stimmen die vorgenommen Näherungen, nämlich Reibung und Gravitation vernachlässigen, im Allgemeinen besser als auf der Erde). Für eine bestimmte Zielgeschwindigkeit ist die benötigte Energie minimal, wenn die Ausströmgeschwindigkeit 62,75 % der Zielgeschwindigkeit beträgt.
Für Raketenstarts von der Erde muss die Formel um die Erdanziehungskraft ergänzt werden und lautet für geringe Steighöhen mit einer konstanten Fallbeschleunigung
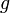 von 9,81 m/s²:
von 9,81 m/s²:Da
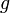 von der Höhe abhängt, heißt es mit dieser Korrektur:
von der Höhe abhängt, heißt es mit dieser Korrektur:Außer der Erdanziehung muss eine von der Erde startende Rakete auch noch den Luftwiderstand der Atmosphäre überwinden, weshalb die Raketengrundgleichung für diesen Fall nur näherungsweise gilt. Außerdem ist die Rotationsgeschwindigkeit der Erde noch nicht berücksichtigt, die im günstigsten Fall etwa 0,46 km/s beiträgt.
Flugzeuge, die durch Strahltriebwerke angetrieben werden, führen zwar ihren Brennstoff mit, saugen aber Luft an, verwenden deren Sauerstoff für die Verbrennung des Treibstoffs und stoßen das entstehende heiße Gasgemisch aus. Sie führen also nur einen Teil ihrer Antriebsmasse mit sich. Für solche Flugkörper gilt die Raketengrundgleichung nicht.
Bei Swing-by-Manövern gilt die Raketengrundgleichung ebenfalls nicht, weil der Impuls des ablenkenden Körpers mit berücksichtigt werden muss. Das gleiche gilt für geplante Antriebe, die das Magnetfeld der Erde oder Sonne nutzen sollen.
Die Raketengrundgleichung setzt auf die klassische Mechanik auf, gilt also nicht für Geschwindigkeiten nahe der Lichtgeschwindigkeit. In der heutigen Raumfahrt werden jedoch nur etwa 0,01 % der Lichtgeschwindigkeit erreicht, so dass relativistische Effekte vernachlässigt werden können.
Quellen
- Bernd Leitenberger: Die Raketengrundgleichung. Abgerufen am 12. Dezember 2008.
- Herleitung der Raketengrundgleichnung (englisch)
Wikimedia Foundation.