Randpunkt

Im mathematischen Teilgebiet der Topologie ist der Begriff Rand eine Abstraktion der anschaulichen Vorstellung einer Begrenzung eines Bereiches. Formal ist der Rand einer Teilmenge U eines topologischen Raumes die Differenzmenge zwischen Abschluss und Innerem von U. Der Rand einer Menge U wird üblicherweise mit 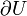$\partial U$ bezeichnet, also:

$\partial U = \overline{U} \setminus U^\circ$.

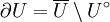Damit verwandte aber abweichende Randbegriffe gibt es in der algebraischen Topologie und in der Theorie von Mannigfaltigkeiten.

Eigenschaften

• Der Rand einer Menge ist stets abgeschlossen.
• Der Rand einer Menge U besteht genau aus den Punkten, für die gilt, dass jede ihrer Umgebungen sowohl Punkte aus U als auch Punkte, die nicht in U liegen, enthält.
• Der Rand einer Menge ist stets gleich dem Rand ihres Komplements.
• Der Rand einer Menge ist der Schnitt des Abschlusses der Menge mit dem Abschluss ihres Komplementes.
• Eine Menge ist genau dann abgeschlossen, wenn sie ihren Rand enthält.
• Eine Menge ist genau dann offen, wenn sie zu ihrem Rand disjunkt ist.
• Eine Menge ist genau dann offen und abgeschlossen, wenn ihr Rand leer ist.
• Es seien X ein topologischer Raum, 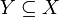$Y\subseteq X$ eine offene Teilmenge mit der Teilraumtopologie und 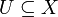$U\subseteq X$ eine Teilmenge. Dann ist der Rand von 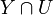$Y\cap U$ in Y gleich dem Schnitt von Y mit dem Rand von U in X. Lässt man die Voraussetzung der Offenheit von Y fallen, so gilt die entsprechende Aussage selbst dann nicht, wenn U eine Teilmenge von Y ist, wie das Beispiel 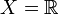$X=\mathbb R$, U = Y = {0} zeigt.

Beispiele

• Ist U eine offene oder abgeschlossene Kreisscheibe in der Ebene 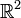$\mathbb R^2$, so ist der Rand von U die zugehörige Kreislinie.
• Der Rand von $\mathbb Q$ als Teilmenge von $\mathbb R$ ist ganz $\mathbb R$.