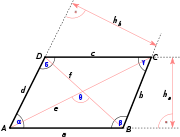
Rhomboid

Formeln zum Parallelogramm
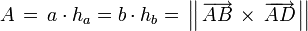
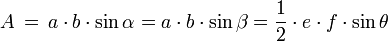
Flächeninhalt	$A \, = \, a \cdot h_a = b \cdot h_b = \, \left| \left|\,\overrightarrow{AB} \, \times \, \overrightarrow{AD}\,\right| \right|$ $A \, = \, a \cdot b \cdot \sin\alpha = a \cdot b \cdot \sin\beta = \frac{1}{2} \cdot e \cdot f \cdot \sin \theta$
Höhe zu a	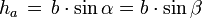$h_a \, = \, b \cdot \sin\alpha = b \cdot \sin\beta$
Höhe zu b	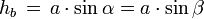$h_b \, = \, a \cdot \sin\alpha = a \cdot \sin\beta$
Diagonalen (Kosinussatz)	$f = \sqrt{ a^2+d^2-2 \cdot a \cdot d \cdot \cos (\alpha) }$ $e = \sqrt{ a^2+d^2+2 \cdot a \cdot d \cdot \cos (\alpha) }$
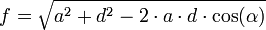
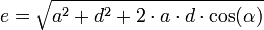
Winkel	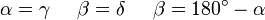$\alpha = \gamma \;\;\;\;\; \beta = \delta \;\;\;\;\; \beta = 180^\circ - \alpha$
Seitenlängen	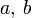$a,\,b$
Größen der Innenwinkel	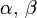$\alpha,\,\beta$

Bezeichnungen am Parallelogramm

Ein Parallelogramm oder Rhomboid (rautenähnlich) ist ein konvexes ebenes Viereck, bei dem gegenüberliegende Seiten parallel sind.

Äquivalent dazu sind zahlreiche andere Eigenschaften, die in der folgenden Charakterisierung zusammengefasst sind: Ein nicht ausgeartetes Viereck ist ein Parallelogramm genau dann, wenn eine der folgenden Bedingungen erfüllt ist:

• Gegenüberliegende Seiten sind gleich lang und keine zwei gegenüberliegende Seiten schneiden sich (kein überschlagenes Viereck).
• Gegenüberliegende Winkel sind gleich groß.
• Je zwei benachbarte Winkel ergeben zusammen 180°.
• Die Diagonalen halbieren einander.
• Es ist punktsymmetrisch (zweizählig drehsymmetrisch).

Für jedes Parallelogramm gilt:

• Jede Diagonale teilt es in zwei (gleich orientierte) kongruente Dreiecke.
• Das Zentrum der Symmetrie ist der Schnittpunkt der Diagonalen.

Rechteck, Rhombus (Raute) und Quadrat sind Spezialfälle des Parallelogramms. Parallelogramme sind spezielle Trapeze.

Parallelogramme sind zweidimensionale Parallelepipede.

Im Parallelogramm gilt das Parallelogrammgesetz: $e^2+f^2 = 2\left(a^2+b^2\right)$.

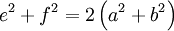Weblinks

Konvexe Vierecke

Quadrat | Rechteck | Raute | Parallelogramm | Drachenviereck | Trapez | Sehnenviereck | Tangentenviereck