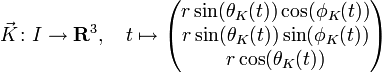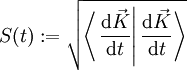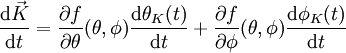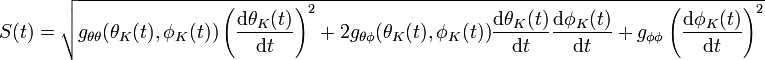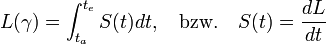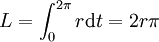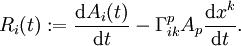- Riemannscher Raum
-
Die riemannsche Geometrie ist ein Teilgebiet der Differentialgeometrie.
Historisch gesehen wurde dieses Teilgebiet der Mathematik ausgehend von den Arbeiten von Carl Friedrich Gauß durch Bernhard Riemann entwickelt. Die riemannsche Geometrie beschäftigt sich im Gegensatz zu den früheren Arbeiten von Gauß auch mit höherdimensionalen, topologischen Räumen. Während Gauß also die Theorie der gekrümmten, zweidimensionalen Flächen im dreidimensionalen euklidischen Raum entwickelte, löste sich Riemann vom Gedanken der eingebetteten Flächen und beschränkte sich auf die mathematische Beschreibung der geometrischen Eigenschaften n-dimensionaler Flächen.
Diese riemannschen Mannigfaltigkeiten oder riemannschen Räume lassen sich sehr oft über geeignete Parametrisierungen darstellen und untersuchen. Die Definitionsbereiche dieser Parameter bilden dabei ebenfalls riemannsche Mannigfaltigkeiten. Solche Definitionsbereiche werden dann durch eine Abbildung, die jedem Element der Menge eine riemannsche Metrik zuordnet, zu einer riemannschen Mannigfaltigkeit. Mit Hilfe der Metrik lassen sich dann die wesentlichen geometrischen Eigenschaften der Mannigfaltigkeit beschreiben. So gelten auf jeder gekrümmten zweidimensionalen Fläche und auch den höherdimensionalen gekrümmten Gebilde die folgenden, teilweise identischen, Eigenschaften:
- Die kürzesten Strecken zwischen unterschiedlichen Punkten (die sogenannten Geodäten) sind nicht zwingend Geradenstücke, sondern können gekrümmte Kurven sein
- Die Winkelsumme von Dreiecken kann, im Gegensatz zur Ebene, auch größer (z.B. Kugel) oder kleiner (hyperbolische Räume) als 180° sein
- Die Parallelverschiebung von Tangentialvektoren entlang geschlossener Kurven kann die Richtung des Vektors ändern
- Das Ergebnis einer Parallelverschiebung eines Tangentialvektors hängt auch vom Weg ab, entlang dessen der Tangentialvektor verschoben wird
- Die Krümmung der Fläche, bzw. des n-dimensionalen Gebildes, ist im Allgemeinen vom Ort auf der Fläche abhängig
- Abstandsmessungen zwischen unterschiedlichen Punkten der Fläche sind nur mit Hilfe einer Metrik möglich, die vom Ort auf der Fläche abhängen kann
Der etwas allgemeinere Begriff der pseudo-riemannschen oder semi-riemannschen Mannigfaltigkeit ist in der allgemeinen Relativitätstheorie von entscheidender Bedeutung, da die Raumzeit als solche beschrieben wird.
Inhaltsverzeichnis
Mathematische Definition
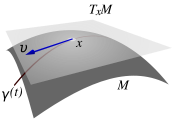
Eine riemannsche Mannigfaltigkeit ist eine differenzierbare n-dimensionale Mannigfaltigkeit M mit einer Funktion g, die in jedem Punkt
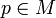 ein Skalarprodukt des Tangentialraums TpM definiert. g ist also eine positiv definite, symmetrische Bilinearform
ein Skalarprodukt des Tangentialraums TpM definiert. g ist also eine positiv definite, symmetrische Bilinearform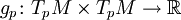 ,
,
die differenzierbar von p abhängt, d.h., bei gegebenen differenzierbaren Vektorfeldern
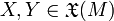 ist
isteine differenzierbare Funktion.
Die Funktion g heißt riemannsche Metrik oder auch metrischer Tensor, ist aber keine Metrik im Sinne der metrischen Räume. Man kann aber mit Hilfe von g eine Metrik im Sinne der metrischen Räume wie folgt definieren:
Dabei durchläuft γ alle differenzierbaren Wege, die x und y verbinden, und L(γ) bezeichnet die Länge von γ, die gemäß
definiert ist. Die so definierte Metrik d induziert wieder die ursprüngliche Topologie von M. Weil man zeigen kann, dass jede differenzierbare n-dimensionale Mannigfaltigkeit riemannsche Metriken besitzt, bedeutet dies, dass jede differenzierbare n-dimensionale Mannigfaltigkeit metrisierbar ist.
Ein Weg, der lokal (d.h. für ausreichend nahe beieinander liegende Punkte) die kürzeste Verbindung realisiert, heißt Geodätische.
Beispiele
Menge der reellen n-Tupel
Gemäß Definition ist die Menge aller n-Tupel der reellen Zahlen
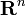 zusammen mit dem euklidischen Standardskalarprodukt eine riemannsche Mannigfaltigkeit. Der Tangentialraum des
zusammen mit dem euklidischen Standardskalarprodukt eine riemannsche Mannigfaltigkeit. Der Tangentialraum des 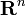 ist in diesem Beispiel identisch mit dem Ausgangsraum, also wieder der
ist in diesem Beispiel identisch mit dem Ausgangsraum, also wieder der 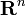 .
.Untermannigfaltigkeiten
An dem Beispiel einer zweidimensionalen Kugeloberfläche lassen sich weitere grundlegende Definitionen der riemannschen Geometrie veranschaulichen. Wird die Kugeloberfläche als eingebetter Unterraum des
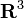 betrachtet, wird unmittelbar klar, dass die Menge aller Punkte auf der Kugeloberfläche eine Untermenge des
betrachtet, wird unmittelbar klar, dass die Menge aller Punkte auf der Kugeloberfläche eine Untermenge des 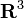 ist. Dieser Raum ist, wie gerade beschrieben, zusammen mit der euklidischen Norm eine riemannsche Mannigfaltigkeit. Da nun der Tangentialraum eines jeden Punktes der Kugeloberfläche ebenfalls eine Teilmenge des Einbettungsraumes
ist. Dieser Raum ist, wie gerade beschrieben, zusammen mit der euklidischen Norm eine riemannsche Mannigfaltigkeit. Da nun der Tangentialraum eines jeden Punktes der Kugeloberfläche ebenfalls eine Teilmenge des Einbettungsraumes 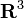 ist, kann das Skalarprodukt des Einbettungsraumes für diese Teilmenge ebenfalls als Skalarprodukt, bzw. Metrik verwendet werden. Diese neue Metrik für den Tangentialraum der Kugeloberfläche wird auch induzierte Metrik genannt. Da diese Definition der induzierten Metrik auf alle Punkte der Kugeloberfläche anwendbar ist, wird die Menge aller Punkte auf der Kugeloberfläche damit zu einer riemannschen Untermannigfaltigkeit. Mit dieser induzierten Metrik läßt sich nun die Länge einer beliebigen differenzierbaren, stetigen Kurve auf der Kugeloberfläche berechnen. Über Kugelkoordinaten wird dazu eine bijektive Abbildung einer geeigneten Teilmenge der Kugeloberfläche in den
ist, kann das Skalarprodukt des Einbettungsraumes für diese Teilmenge ebenfalls als Skalarprodukt, bzw. Metrik verwendet werden. Diese neue Metrik für den Tangentialraum der Kugeloberfläche wird auch induzierte Metrik genannt. Da diese Definition der induzierten Metrik auf alle Punkte der Kugeloberfläche anwendbar ist, wird die Menge aller Punkte auf der Kugeloberfläche damit zu einer riemannschen Untermannigfaltigkeit. Mit dieser induzierten Metrik läßt sich nun die Länge einer beliebigen differenzierbaren, stetigen Kurve auf der Kugeloberfläche berechnen. Über Kugelkoordinaten wird dazu eine bijektive Abbildung einer geeigneten Teilmenge der Kugeloberfläche in den 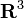 definiert.
definiert.Der Wertebereich dieser Funktion entspricht dabei gerade einer Kugeloberfläche mit Radius r, aber ohne Nord- und Südpol:
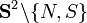 . Die Funktion f wird in der Literatur normalerweise Parametrisierung, die Umkehrfunktion von f dagegen Karte, der Kugeloberfläche genannt.
. Die Funktion f wird in der Literatur normalerweise Parametrisierung, die Umkehrfunktion von f dagegen Karte, der Kugeloberfläche genannt.Der Tangentialraum des Punktes p = f(θ,φ) ist in diesem Beispiel die Tangentialebene an der Kugeloberfläche durch diesen Punkt. Die partiellen Ableitungen von f
sind deshalb Elemente des Tangentialraumes. Da beide Vektoren über dem gesamten Definitionsbereich linear unabhängig sind, bilden sie für jeden Punkt des Definitionsbereiches auch eine Basis für alle Elemente des Tangentialbündels. Mit dieser Basis existiert deshalb auch eine Koordinatendarstellung der induzierten, riemannschen Metrik. Dazu werden alle vier Skalarprodukte dieser Basisvektoren berechnet
und
Aufgrund der Symmetrie des Skalarproduktes sind die beiden Funktionen gθφ und gφθ identisch.
Diese Komponentendarstellung der Metrik wird in der theoretischen Physik auch metrischer Tensor genannt. Die Indizes i und j können beide die Werte 1 oder 2 annehmen. Dabei steht die Ziffer 1 für die erste Koordinate θ und 2 für die zweite Koordinate φ.
Berechnung von Längen auf der Kugeloberfläche
Anhand der Kugeloberfläche lässt sich gut zeigen, wie Entfernungen auf eingebetteten Räumen berechnet werden können. Mit Hilfe zweier Funktionen
im Parameterraum
![{]0,\pi[} \times {[0,2\pi[}\subset \mathbf{R}^2](/pictures/dewiki/50/2fb85b2fa60f19a4b9a32f34f401867e.png) des obigen Beispiels definiert. I ist dabei ein geeignetes Intervall in
des obigen Beispiels definiert. I ist dabei ein geeignetes Intervall in 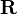 . Durch Einsetzen in die Definition der Kugelkoordinaten wird eine Kurve auf der Kugeloberfläche definiert:
. Durch Einsetzen in die Definition der Kugelkoordinaten wird eine Kurve auf der Kugeloberfläche definiert:Die Ableitung
 ist gerade der Tangentialvektor an die Kurve
ist gerade der Tangentialvektor an die Kurve 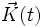 . Mit Hilfe des euklidischen Skalarprodukts kann die Länge dieses Vektors berechnet werden:
. Mit Hilfe des euklidischen Skalarprodukts kann die Länge dieses Vektors berechnet werden:Die totale Ableitung nach t berechnet sich ganz allgemein gemäß:
Daraus folgt mit den Bezeichnungen des obigen Beispiels der Kugeloberfläche die folgende Gleichung:
Auf der rechten Seite des Gleichheitszeichens steht aber gerade der Integrand aus der Definition von L(γ). Die Integration ergibt somit den Abstand zwischen beliebigen Punkten auf der Kugeloberfläche ohne Nord- und Südpol:
Nun kann auch der Umfang der Kugel, als Länge des Äquators, berechnet werden. Mit
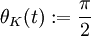 und φK(t): = t mit
und φK(t): = t mit 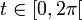 wird der Äquator der Kugel geeignet parametrisiert und es gilt
wird der Äquator der Kugel geeignet parametrisiert und es giltDie Integration dieser Gleichung ergibt die richtige Formel für den Umfang bzw. die Länge des Äquators der Kugeloberfläche.
Die mathematische Entfernungsmessung funktioniert hier nach dem physikalischen Prinzip der Momentangeschwindigkeit. Die Länge des Weges ergibt sich dabei durch Integration der momentanen Geschwindigkeiten, mit denen der Weg beschritten wird, multipliziert mit infinitesimal kleinen Zeitabschnitten dt.
Richtungsableitung und Parallelverschiebung von Tangentialvektoren
Bei der Definition der Richtungsableitung ist es sehr praktisch, auch wieder von eingebetteten zweidimensionalen Flächen auszugehen. Die Ergebnisse lassen sich dann sehr leicht auf n-dimensionale Mannigfaltigkeiten verallgemeinern.
Um die Richtungsableitung von Tangentialvektoren zu definieren, denkt man sich, genau wie in dem eben dargestellten Beispiel, eine beliebige Kurve auf der Fläche und die zugehörigen Tangentialvektoren an diese Kurve. Diese Tangentialvektoren existieren dabei sowohl als dreidimensionale Vektoren des umgebenden euklidischen Raumes als auch als zweidimensionale Vektoren in der Tangentialebene. Im Fall der zweidimensionalen Fläche ist der dreidimensionale Tangentialvektor einfach die Ableitung der dreidimensionalen Kurvenfunktion nach dem Parameter t. Dies ist soweit analog zu obigem Beispiel, wo Distanzen auf der Fläche berechnet werden. Der Vektor
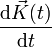 ist also für jedes t ein Tangentialvektor, sofern
ist also für jedes t ein Tangentialvektor, sofern 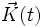 auch in der Fläche bzw. Mannigfaltigkeit liegt. Nun ist der naheliegendste Ansatz für eine Richtungsableitung einfach die zweite Ableitung
auch in der Fläche bzw. Mannigfaltigkeit liegt. Nun ist der naheliegendste Ansatz für eine Richtungsableitung einfach die zweite Ableitung 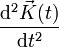 . Dieser Vektor kann ebenfalls entlang der Kurve und für jedes t berechnet werden, doch muss dabei beachtet werden, dass dieser neue Vektor normalerweise kein Tangentialvektor mehr ist. Dies kann jedoch durch eine Projektion auf die Tangentialebene gewährleistet werden. Damit ergibt sich wieder ein Vektor, der in der Tangentialebene liegt. Dieser Vektor wird auch als Richtungsableitung des Tangentialvektors bezeichnet. Sind alle partiellen Ableitungen der Metrik stetig, so kann diese Projektion alleine über die induzierte Metrik berechnet werden. Die konkrete Rechnung zeigt, dass in die Formel für die Richtungsableitung dann nur noch die Koordinatendarstellung der induzierten Metrik eingeht. Damit erhält diese Formel ihre Bedeutung für die riemannschen Mannigfaltigkeiten. Für die Richtungsableitung der Tangentialvektoren gilt also
. Dieser Vektor kann ebenfalls entlang der Kurve und für jedes t berechnet werden, doch muss dabei beachtet werden, dass dieser neue Vektor normalerweise kein Tangentialvektor mehr ist. Dies kann jedoch durch eine Projektion auf die Tangentialebene gewährleistet werden. Damit ergibt sich wieder ein Vektor, der in der Tangentialebene liegt. Dieser Vektor wird auch als Richtungsableitung des Tangentialvektors bezeichnet. Sind alle partiellen Ableitungen der Metrik stetig, so kann diese Projektion alleine über die induzierte Metrik berechnet werden. Die konkrete Rechnung zeigt, dass in die Formel für die Richtungsableitung dann nur noch die Koordinatendarstellung der induzierten Metrik eingeht. Damit erhält diese Formel ihre Bedeutung für die riemannschen Mannigfaltigkeiten. Für die Richtungsableitung der Tangentialvektoren gilt alsoÜber alle doppelten Indizes wird hier gemäß der einsteinschen Summenkonvention summiert. Die Funktionen
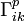 heißen Christoffelsymbole. Sie lassen sich aus der Metrik durch partielle Ableitung berechnen. Zu beachten bleibt, dass sich diese Formel nur noch auf die riemannsche Mannigfaltigkeit bzw. die Tangentialebenen bezieht. Im Falle einer zweidimensionalen Fläche nimmt jeder Index also die Werte 1 und 2 an. Bezogen auf obiges Beispiel der Kugeloberfläche ist Ai(t) die zweidimensionale Koordinatendarstellung des Vektors
heißen Christoffelsymbole. Sie lassen sich aus der Metrik durch partielle Ableitung berechnen. Zu beachten bleibt, dass sich diese Formel nur noch auf die riemannsche Mannigfaltigkeit bzw. die Tangentialebenen bezieht. Im Falle einer zweidimensionalen Fläche nimmt jeder Index also die Werte 1 und 2 an. Bezogen auf obiges Beispiel der Kugeloberfläche ist Ai(t) die zweidimensionale Koordinatendarstellung des Vektors 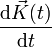 . Zudem gilt
. Zudem giltSind für alle definierten t alle Komponenten der Richtungsableitung Ri(t) gleich null, wird der Vektor
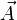 entlang der Kurve K parallel verschoben. Ist
entlang der Kurve K parallel verschoben. Ist 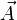 zusätzlich der Tangentialvektor der Kurve K für alle t, so ist diese Kurve auch die kürzeste Verbindung zwischen Anfangs- und Endpunkt der Kurve. Solche Kurven werden, wie bereits oben erwähnt, Geodäten genannt.
zusätzlich der Tangentialvektor der Kurve K für alle t, so ist diese Kurve auch die kürzeste Verbindung zwischen Anfangs- und Endpunkt der Kurve. Solche Kurven werden, wie bereits oben erwähnt, Geodäten genannt.Die Richtungsableitung wird in der Fachliteratur üblicherweise als kovariante Ableitung bezeichnet.
Geschichte
Gauß’ Theorie der gekrümmten Flächen verwendet eine extrinsische Beschreibung, d.h., die gekrümmten Flächen werden mit Hilfe eines umgebenden, euklidischen Raumes beschrieben. Riemann vertritt dagegen einen abstrakteren Ansatz, der ohne umgebende Räume auskommt. Diesen Ansatz und die zugehörigen Definitionen führte Riemann in seinem Habilitationsvortrag Über die Hypothesen, welche der Geometrie zu Grunde liegen vom 10. Juni 1854 an der Universität Göttingen ein. Dort wurden auch viele Definitionen vorgestellt, die noch heute in der modernen Mathematik verwendet werden. Von parakompakten Räumen war damals jedoch noch nicht die Rede. Anstelle von Kurven und Tangentialvektoren verwendete Riemann damals infinitesimale Linienelemente.
Seit Anfang des 19. Jahrhunderts werden so genannte nichteuklidische Geometrien diskutiert. Die riemannsche Geometrie hat dabei gerade die geeigneten Definitionen und die geeignete Sprache, um diese Geometrien von einem allgemeinen Standpunkt aus zu beschreiben. Der Begriff der riemannschen Mannigfaltigkeit bildete zum Anfang des 20. Jahrhunderts einen grundlegenden Ausgangspunkt für die Entwicklung der allgemeinen Relativitätstheorie.
Siehe auch
Literatur
- Manfredo Perdigão do Carmo: Riemannian Geometry, Birkhäuser, Boston 1992, ISBN 0-8176-3490-8
- Sylvestre Gallot, Dominique Hulin, Jacques Lafontaine: Riemannian Geometry (Second Edition), Springer-Verlag, Berlin/Heidelberg 1990, ISBN 3-540-52401-0
- Martin Schottenloher: Geometrie und Symmetrie in der Physik, vieweg Lehrbuch, 1995, ISBN 3-528-06565-6
- Torsten Fließbach: Allgemeine Relativitätstheorie, Spektrum Akademischer Verlag, Heidelberg 2006, ISBN 3-8274-1356-7
- Siegfried Kästner: Vektoren, Tensoren, Spinoren, Akademie Verlag, Berlin 1964
Weblinks
- Bernhard Riemann: Ueber die Hypothesen, welche der Geometrie zu Grunde liegen, Inauguralvorlesung, Thema von Carl Friedrich Gauß vorgeschlagen
Wikimedia Foundation.

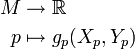
![d(x,y):=\inf\{L(\gamma)\mid\gamma\colon[0,1]\to M,\gamma(0)=x, \gamma(1)=y\}](/pictures/dewiki/56/824f056db07f4e6f1188585cdb030f5d.png)

![f\colon {]0,\pi[} \times [0,2\pi[ \to \mathbf{R}^3, \quad (\theta,\phi) \mapsto
\begin{pmatrix}
r\sin(\theta)\cos(\phi)\\
r\sin(\theta)\sin(\phi)\\
r\cos(\theta)
\end{pmatrix}](/pictures/dewiki/51/30c8a5d9c18257320056e6f632162c05.png)
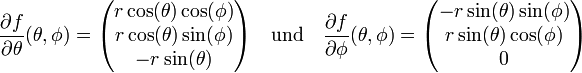

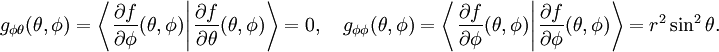
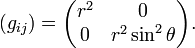
 definiert als Geschwindigkeitsvektor einer Kurve
definiert als Geschwindigkeitsvektor einer Kurve ![\theta _{K} \colon I \to {]0,\pi[} \quad \mbox{und} \quad \phi _{K} \colon I \to {[0,2\pi[}
\quad \mbox{wird eine Kurve} \quad t \mapsto (\theta_K(t), \phi_K(t))](/pictures/dewiki/100/daedecdcf9495f01624bae995753135c.png)