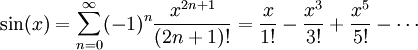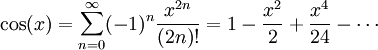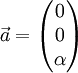- Rodriguez-Formel
-
Die Rodrigues-Formel ist eine Formel für die einer antisymmetrischen 3*3 Matrix, welche in Matrixform ein Kreuzprodukt beschreibt. Sie lautet :
Ihre Hauptanwendung, liegt darin, dass das Ergebnis eine Drehung um Achse a mit Winkel
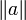 als Matrix beschreibt.
als Matrix beschreibt.Inhaltsverzeichnis
Herleitung
Die Exponentialfunktion lässt sich in eine unendliche , die für alle Werte aus
 , darstellen als:
, darstellen als:Die Gleichung kann auch für beliebige quadratische angewendet werden. Eine, die sich wegen ihrer besonderen Eigenschaften dafür eignet ist die Matrix des . Sie lautet für den dreidimensionalen, reellen Raum
 :
:Mit einer Matrixmultiplikation lässt sich folgende Gleichung auflösen :
Das bedeutet, dass eine Matrix mit einem beliebigem Exponenten, der größer 2 ist, reduziert werden kann.
Für und gibt es ebenfalls Taylorentwicklungen. Sie lauten :
Diese Gleichungen können kombiniert werden : Terme mit geradem Exponenten können durch die Cosinus-Entwicklung und Terme mit ungeradem Exponenten durch die Sinus-Entwicklung ersetzt werden. Nach einigen Vereinfachungen erhält man die Rodriguez-Gleichung.
Eigenschaften
Sei
![R(x) = \exp([a]_{\times})](/pictures/dewiki/57/919317e0186437c4e5d978946a98cc40.png) . Dann gilt :
. Dann gilt :- R( − x) = R(x) − 1 = R(x)T
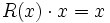
Anwendung
Vor allem in der und in der spielt die Rodriguezformel eine Rolle. Es existiert immer ein Koordinatensystem, definiert durch
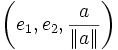 , in dem für einen Vektor
, in dem für einen Vektor 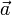 gilt:
gilt:Das bedeutet, dass die Matrix
![\exp([a]_{\times})](/pictures/dewiki/54/69591e25faadd272bd7355acd1a33f45.png) eine Rotation um die Achse
eine Rotation um die Achse 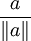 repräsentiert. Der Drehwinkel ist dabei
repräsentiert. Der Drehwinkel ist dabei 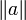 , also die Länge des Vektors.
, also die Länge des Vektors.Literatur
- Ismail, M.E.H.: Classical and Quantum Orthogonal Polynomials in One Variable. Cambridge UK: Cambridge University Press, 2005. ISBN 978-0-521-78201-2
- Faugeras, O.: Three-Dimensional Computer Vision - A Geometric Viewpoint. Cambridge MA: MIT Press, 1993. ISBN 978-0-262-06158-2
Wikimedia Foundation.

![\exp([a]_{\times}) =
I + \sin(\|a\|) \begin{bmatrix}\dfrac{a}{\|a\|}\end{bmatrix}_{\times} +
(1 - \cos(\|a\|)) \begin{bmatrix}\dfrac{a}{\|a\|}\end{bmatrix}_{\times}^2](/pictures/dewiki/54/64516a323b54dcb19551147b044f8e42.png)
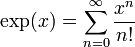
![\vec{a} = \begin{pmatrix}a_1 \\ a_2 \\ a_3\end{pmatrix}
\qquad
[a]_{\times}=
\begin{pmatrix}
0 & -a_3 & a_2 \\
a_3 & 0 & -a_1 \\
-a_2 & a_1 & 0
\end{pmatrix}](/pictures/dewiki/52/41ff606e47a166734ee62ff5ec6015cb.png)
![[a]_{\times}^3 = [a]_{\times} \cdot [a]_{\times} \cdot [a]_{\times} = - \|a\|^2 \cdot [a]_{\times}](/pictures/dewiki/102/f34e9ee93a6ee8277acf83950f62cbe1.png)