Satz von Fejer

In der Mathematik ist der Satz von Fejér (nach Leopold Fejér) eine der wichtigsten Aussagen über die Konvergenz von Fourierreihen. Der Satz besagt, dass die arithmetischen Mittel der Partialsummen der Fourierreihe einer stetigen, 2π-periodischen Funktion gleichmäßig gegen die Funktion konvergieren.

Mathematische Formulierung

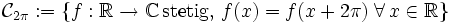$\mathcal{C}_{2\pi} := \left\{ f : \mathbb{R} \rightarrow \mathbb{C} \, \mbox{stetig}, \, f(x) = f(x+2\pi) \; \forall \, x \in \mathbb{R} \right\}$ sei der Raum der stetigen 2π-periodischen Funktionen.

Die n-te Partialsumme 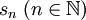$s_n \; (n \in \mathbb{N})$ der Fourierreihe einer Funktion 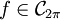$f \in \mathcal{C}_{2\pi}$ ist gegeben durch 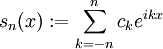$s_n(x) := \sum_{k=-n}^n c_k e^{ikx}$, mit den Fourierkoeffizienten $c_k := \frac{1}{2\pi} \int_0^{2\pi} f(x) e^{-ikx} \mathrm{d}x$.

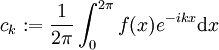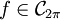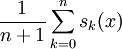Der Satz von Fejér lautet nun formal: Für $f \in \mathcal{C}_{2\pi}$ gilt: $\frac{1}{n+1} \sum_{k=0}^n s_k(x)$ konvergiert für 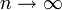$n \rightarrow \infty$ gleichmäßig in $\mathbb{R}$ gegen f(x).

Der Satz von Fejér kann in dieser Form nicht weiter verschärft werden:

• Leopold Fejér konstruierte 1911 ein Beispiel einer Funktion 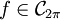$f \in \mathcal{C}_{2\pi}$, deren Fourierreihe in wenigstens einem Punkt nicht konvergiert.
• Wird die Bedingung der Stetigkeit zu stückweiser Stetigkeit abgeschwächt, konvergieren auch die arithmethischen Mittel der Partialsummen in den Unstetigkeitsstellen nicht mehr gegen den Funktionswert.

Konsequenzen

• Falls eine Fourierreihe einer Funktion aus 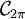$\mathcal{C}_{2\pi}$ in einem Punkt konvergiert, dann konvergiert sie gegen den Funktionswert.

• Die Fourierreihenentwicklung ist eindeutig: Zwei Funktionen aus 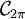$\mathcal{C}_{2\pi}$ haben genau dann die gleiche Fourierreihe, wenn sie als Funktionen übereinstimmen.

• Die Partialsummen einer Funktion 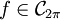$f \in \mathcal{C}_{2\pi}$ konvergieren in der 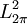$L^2_{2\pi}$-Norm gegen die Funktion, d. h. für 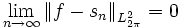$\lim_{n \rightarrow \infty} \left\| f - s_n \right\|_{L^2_{2\pi}} = 0$, wobei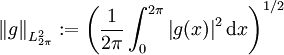 $\left\|g\right\|_{L^2_{2\pi}} := \left( \frac{1}{2\pi} \int_0^{2\pi} \left|g(x)\right|^2 \mathrm{d}x \right)^{1/2}$

• Für 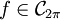$f \in \mathcal{C}_{2\pi}$ gilt die sogenannte Bessel-Gleichung: 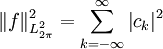$\left\| f \right\|_{L^2_{2\pi}}^2 = \sum_{k=-\infty}^\infty \left|c_k\right|^2$, wobei c_k die Fourierkoeffizienten von f sind.

• Durch Polarisieren erhält man aus der Bessel-Gleichung den Satz von Parseval: Seien 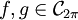$f, g \in \mathcal{C}_{2\pi}$ mit Fourierkoeffizienten c_k bzw. d_k. Dann gilt: 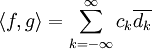$\langle f, g \rangle = \sum_{k=-\infty}^\infty c_k \overline{d_k}$, wobei 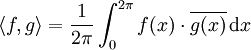$\langle f, g \rangle = \frac{1}{2\pi} \int_{0}^{2\pi} f(x) \cdot \overline{g(x)} \, \mathrm{d}x$ das Standard-Skalarprodukt ist.